Question

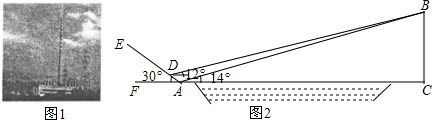
3．恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世，著名的恩施大峡谷A和世界级自然保护区星斗山B位于笔直的沪渝高速公路X同侧，AB=50km，A、B到直线X的距离分别为10km和40km，要在沪渝高速公路旁修建一服务区P，向A、B两景区运送游客，小民设计了两种方案，图（1）是方案一的示意图（AP与直线X垂直，垂足为P），点P到A、B的距离之和S₁=PA+PB，图（2）是方案二的示意图（点A关于直线X的对称点是A′，连接BA'交直线X于点P），点P到A、B的距离之和S₂=PA+PB．
（1）求S₁、S₂，并比较它们的大小；
（2）请你说明S₂=PA+PB的值为最小．

Answer 1

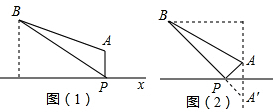
分析 （1）根据勾股定理分别求得S₁、S₂的值，比较即可；
（2）在公路上任找一点M，连接MA，MB，MA'，由轴对称知MA=MA，于是得到MB+MA=MB+MA'＞A'B，即可得到S₂=BA'为最小．

解答 解：（1）图（1）中过B作BC⊥X于C，垂足为C；AD⊥BC于D，垂足为D，
则BC=40，
又∵AP=10，
∴BD=BC-CD=40-10=30．
在△ABD中，AD=$\sqrt{5{0}^{2}-3{0}^{2}}$=40，
在Rt△PBC中，
∴BP=$\sqrt{C{P}^{2}+B{C}^{2}}$=10$\sqrt{40}$，
S₁=40$\sqrt{2}$+10．
图（2）中，过B作BC⊥AA′垂足为C，则A′C=50，
又∵BC=40，
∴BA'=$\sqrt{4{0}^{2}+5{0}^{2}}$=10$\sqrt{41}$，
由轴对称知：PA=PA'，
∴S₂=BA'=10$\sqrt{41}$，
∴S₁＞S₂．

（2）如图（2），在公路上任找一点M，连接MA，MB，MA'，由轴对称知MA=MA'，
∴MB+MA=MB+MA'＞A'B，
∴S₂=BA'为最小．

点评 此题考查了线路最短的问题，确定动点为何位置是关键，综合运用勾股定理的知识．