题目内容
14. 菱形ABCD中,AB=6,∠BAC=45°,M为AB上一定点(AM),N,P分别为BC、AC上的动点,则MP+NP的最小值为6.
菱形ABCD中,AB=6,∠BAC=45°,M为AB上一定点(AM),N,P分别为BC、AC上的动点,则MP+NP的最小值为6.
分析 由菱形ABCD中,∠BAC=45°,得出四边形ABCD是正方形,找出点N关于AC的对称点Q,当M、P、Q三点在一条直线上时,MP+NP=PM+PQ=MQ最小,由此求得答案即可.
解答 解:如图,
∵菱形ABCD中,∠BAC=45°,
∴∠DAB=90°,
∴四边形ABCD是正方形,
点N关于AC的对称点Q,当M、P、Q三点在一条直线上时,MP+NP=PM+PQ=MQ最小为正方形的边长为6.
故答案为:6.
点评 此题考查轴对称-最短路线问题,掌握轴对称图形的性质,菱形的性质,是解决问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
2.在△ABC中,已知a=3$\sqrt{3}$,b=2,∠C=150°,则c=( )
| A. | 49 | B. | 7 | C. | 13 | D. | $\sqrt{13}$ |
19.如表是从左到右以及从上到下都是无限的,其中数字如图所示以一定的规律排列,100在表中共出现了6次
| 1 | 1 | 1 | 1 | 1 | … |
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 3 | 5 | 7 | 9 | |
| 1 | 4 | 7 | 10 | 13 | |
| 1 | 5 | 9 | 13 | 17 | |
| … | … |
 如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.
如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.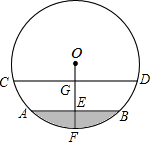 一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)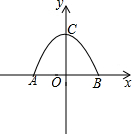 某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.
某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.