题目内容
18.已知函数y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+1.(1)用配方法求抛物线的对称轴和顶点坐标;
(2)画出所给函数的图象;
(3)观察图象,指出当y≤0时,x的取值范围.
分析 (1)根据配方法的操作整理得到顶点式解析式,然后写出对称轴和顶点坐标;
(2)根据二次项系数小于0确定出开口向下,确定出抛物线与x轴的交点坐标,然后作出大致函数图象即可;
(3)根据函数图象写出抛物线在x轴下方部分的x的取值范围.
解答 解:(1)y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+1
=-$\frac{1}{2}$(x2-x+$\frac{1}{4}$)+$\frac{9}{8}$
=-$\frac{1}{2}$(x-$\frac{1}{2}$)2+$\frac{9}{8}$,
抛物线的对称轴为直线x=$\frac{1}{2}$,
顶点坐标为($\frac{1}{2}$,$\frac{9}{8}$);
(2)∵y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+1=-$\frac{1}{2}$(x-2)(x+1),
∴抛物线与x轴的交点坐标为(2,0),(-1,0),且抛物线开口方向向下.
函数图象如图所示;
(3)如图所示:当y≤0时,x的取值范围x≤-1或x≥2.
点评 本题考查了二次函数的三种形式的转化,二次函数图象,二次函数图象与不等式,主要利用了配方法的操作,需熟记.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
6.如果二次三项式ax+3x+4在实数范围内不能分解因式,那么a的取值范围是( )
| A. | 0$<a<\frac{9}{16}$,且a<0 | B. | a≠0 | C. | a$>\frac{9}{16}$ | D. | a$<\frac{3}{4}$且a≠0 |
2.在△ABC中,已知a=3$\sqrt{3}$,b=2,∠C=150°,则c=( )
| A. | 49 | B. | 7 | C. | 13 | D. | $\sqrt{13}$ |
 如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.
如图,△ABC中,∠ACB=90°,AC=BC,点D、E分别在AB、BC上,且CD=DE,作EF⊥AB于点F.若AD=4,BF=2,求△CDE的面积.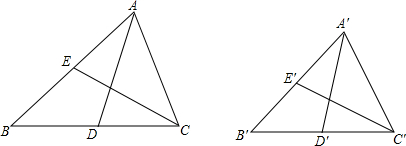
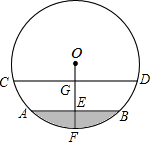 一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)