题目内容

1．如图，在Rt△ABC中，∠A=30°，BC=1，点D，E分别是直角边BC，AC的中点，则DE的长为（　　）
A．1B．2C．$\sqrt{3}$D．1+$\sqrt{3}$

分析 由“30度角所对的直角边等于斜边的一半”求得AB=2BC=2．然后根据三角形中位线定理求得DE=$\frac{1}{2}$AB．

解答 解：如图，∵在Rt△ABC中，∠C=90°，∠A=30°，
∴AB=2BC=2．
又∵点D、E分别是BC，AC的中点，
∴DE是△ACB的中位线，
∴DE=$\frac{1}{2}$AB=1．
故选：A．

点评 此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．

练习册系列答案
相关题目
11．如图1，在四边形ABCD中，E，F分别是CD，AD边上的点，AE=CF，AE，CF相交于点O，连接BE，BF，OB．
（1）如图1，若四边形ABCD是菱形，求证：BE=BF；
（2）在第（1）题的条件下，求证：OB平分∠AOC；
（3）如图2，若四边形ABCD是邻边不等的平行四边形，OB平分∠AOC的结论是否成立？若成立，请你证明；若不成立，请你说明理由．
12．猜想：如图①，在?ABCD中，点O是对角线AC的中点，过点O的直线分别交AD、BC于点E、F．若?ABCD的面积是10，则四边形CDEF的面积是5．
探究：如图②，在菱形ABCD中，对角线AC、BD相交于点O，过点O的直线分别交AD、BC于点E、F．若AC=4，BD=8，求四边形ABFE的面积．
应用：如图③，在Rt△ABC中，∠BAC=90°，延长BC到点D，使DC=BC，连结AD．若AC=4，$AD=\sqrt{73}$，则△ABD的面积是12．
9．算式2.5÷[（$\frac{1}{5}$-1）×（2+$\frac{1}{2}$）]之值为何？（　　）
A．-$\frac{5}{4}$B．-$\frac{125}{16}$C．-25D．11
16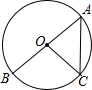．如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则$\widehat{BC}$的长为（　　）
A．$\frac{10}{3}$πB．$\frac{10}{9}$πC．$\frac{5}{9}$πD．$\frac{5}{18}$π
6．下列计算正确的是（　　）
A．3a2-6a2=-3B．（-2a）•（-a）=2a2C．10a10÷2a2=5a5D．-（a3）2=a6
13．如图，四边形ABCD内接于⊙O，F是$\widehat{CD}$上一点，且$\widehat{DF}$=$\widehat{BC}$，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（　　）
A．45°B．50°C．55°D．60°
10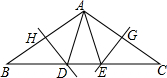．如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（　　）
A．$\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$B．AD，AE将∠BAC三等分
C．△ABE≌△ACDD．S△ADH=S△CEG
11．据统计，2015年广州地铁日均客运量均为6 590 000人次，将6 590 000用科学记数法表示为（　　）
A．6.59×104B．659×104C．65.9×105D．6.59×106

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网