题目内容
16．
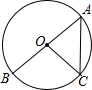如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则$\widehat{BC}$的长为（ ）| A． | $\frac{10}{3}$π | B． | $\frac{10}{9}$π | C． | $\frac{5}{9}$π | D． | $\frac{5}{18}$π |
分析 直接利用等腰三角形的性质得出∠A的度数，再利用圆周角定理得出∠BOC的度数，再利用弧长公式求出答案．
解答 解：∵∠OCA=50°，OA=OC，
∴∠A=50°，
∴∠BOC=100°，
∵AB=4，
∴BO=2，
∴$\widehat{BC}$的长为：$\frac{100π×2}{180}$=$\frac{10}{9}$π．
故选：B．
点评 此题主要考查了弧长公式应用以及圆周角定理，正确得出∠BOC的度数是解题关键．
练习册系列答案
相关题目
6．一个暗箱里放有a个除颜色外完全相同的球，这a个球中红球只有4个，若每次将球搅匀后，任意摸出1个球记下颜色再放回暗箱，通过大量重复摸球实验后发现，摸到红球的频率稳定在20%附近，那么可以推算出a大约是（ ）
| A． | 25 | B． | 20 | C． | 15 | D． | 10 |
如图，在Rt△ABC中，∠C=90°，BC=6，AB=10，则tanA=$\frac{3}{4}$．
4．菱形的两条对角线长分别为6和8，则菱形的周长是（ ）
| A． | 40 | B． | 24 | C． | 20 | D． | 10 |
1．
如图，在Rt△ABC中，∠A=30°，BC=1，点D，E分别是直角边BC，AC的中点，则DE的长为（ ）
如图，在Rt△ABC中，∠A=30°，BC=1，点D，E分别是直角边BC，AC的中点，则DE的长为（ ）| A． | 1 | B． | 2 | C． | $\sqrt{3}$ | D． | 1+$\sqrt{3}$ |
8．以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（ ）
| A． | $\frac{\sqrt{3}}{8}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{2}}{8}$ |
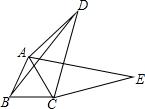如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．线段CD绕点C顺时针旋转60°得到线段CE，连接AE．
如图，转盘中6个小扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向红色区域的概率为$\frac{1}{3}$．