题目内容
11.如图1,在四边形ABCD中,E,F分别是CD,AD边上的点,AE=CF,AE,CF相交于点O,连接BE,BF,OB.(1)如图1,若四边形ABCD是菱形,求证:BE=BF;
(2)在第(1)题的条件下,求证:OB平分∠AOC;
(3)如图2,若四边形ABCD是邻边不等的平行四边形,OB平分∠AOC的结论是否成立?若成立,请你证明;若不成立,请你说明理由.

分析 (1)如图1,过B作BM⊥AE,BN⊥CF,根据菱形的性质得到AB=BC,由于S△ABE=S△BCF=$\frac{1}{2}$S菱形ABCD,得到$\frac{1}{2}$AE•BM=$\frac{1}{2}$CF•BN,推出BM=CN,通过三角形全等得到∠BAM=∠BCN,证得△ABE≌△BCF,根据全等三角形的性质即可得到结论;
(2)由(1)证得BM=BN,根据角平分线的判定定理即可得到结论;
(3)如图2,过B作BM⊥AE,BN⊥CF,根据平行四边形的性质得到S△ABE=S△BCF=$\frac{1}{2}$S四边形ABCD,于是得到$\frac{1}{2}$AE•BM=$\frac{1}{2}$CF•BN,推出BM=CN,根据角平分线的判定定理得到结论.
解答 解:(1)如图1,过B作BM⊥AE,BN⊥CF,
∵四边形ABCD是菱形,
∴AB=BC,
∵S△ABE=S△BCF=$\frac{1}{2}$S菱形ABCD,
∴$\frac{1}{2}$AE•BM=$\frac{1}{2}$CF•BN,
∵AE=CF,
∴BM=CN,
∵BM⊥AE,BN⊥CF,
∴∠AMB=∠BNC=90°,
在Rt△ABM与Rt△BCN中,
$\left\{\begin{array}{l}{AB=BC}\\{BM=BN}\end{array}\right.$,
∴Rt△ABM≌Rt△BCN,
∴∠BAM=∠BCN,
在△ABE与△BCF中,$\left\{\begin{array}{l}{AB=BC}\\{∠BAE=∠BCF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△BCF,
∴BE=BF;
(2)由(1)证得BM=BN,
∵BM⊥AE,BN⊥CF,
∴OB平分∠AOC;
(3)如图2,过B作BM⊥AE,BN⊥CF,
∵四边形ABCD是平行四边形,
∴S△ABE=S△BCF=$\frac{1}{2}$S四边形ABCD,
∴$\frac{1}{2}$AE•BM=$\frac{1}{2}$CF•BN,
∵AE=CF,
∴BM=CN,
∵BM⊥AE,BN⊥CF,
∴OB平分∠AOC;
点评 本题考查了全等三角形的判定和性质,菱形的性质,平行四边形的性质,角平分线的判定,正确的作出辅助线构造全等三角形是解题的关键.

| A. | 25 | B. | 20 | C. | 15 | D. | 10 |
 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
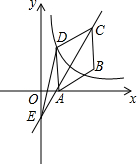 如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=$\frac{k}{x}$(k≠0,x>0)过点D.
如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=$\frac{k}{x}$(k≠0,x>0)过点D.


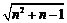 (用含n的代数式表示)
(用含n的代数式表示)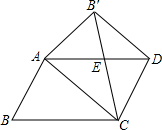 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.