题目内容
13. 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
分析 先根据圆内接四边形的性质求出∠ADC的度数,再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.
解答 解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°-∠ABC=180°-105°=75°.
∵$\widehat{DF}$=$\widehat{BC}$,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC-∠DCE=75°-25°=50°.
故选B.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
相关题目
4.菱形的两条对角线长分别为6和8,则菱形的周长是( )
| A. | 40 | B. | 24 | C. | 20 | D. | 10 |
1. 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
8.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
18.已知,一元二次方程x2-8x+15=0的两根分别是⊙O1和⊙O2的半径,当⊙O1和⊙O2相切时,O1O2的长度是( )
| A. | 2 | B. | 8 | C. | 2或8 | D. | 2<O1O2<8 |
3.已知a-b=2,则代数式2a-2b-3的值是( )
| A. | 1 | B. | 2 | C. | 5 | D. | 7 |

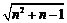 (用含n的代数式表示)
(用含n的代数式表示)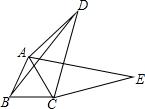 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.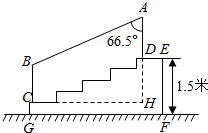 如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)