题目内容
7.已知(m+n)2+|m|=m,且|2m-n-2|=0,求mn的值.分析 由非负数的性质可知:m+n=0,2m-n-2=0,且m≥0,由此联立方程组求得m、n的数值,进一步得出mn的值即可.
解答 解:∵(m+n)2+|m|=m,|2m-n-2|=0,
∴m+n=0,2m-n-2=0且m≥0,
∴$\left\{\begin{array}{l}{m+n=0}\\{2m-n-2=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{2}{3}}\\{n=-\frac{2}{3}}\end{array}\right.$,
∴mn=-$\frac{4}{9}$.
点评 此题考查绝对值的意义,非负数的性质,代数式求值,利用非负数的性质建立方程组求得m、n的数值是关键.

练习册系列答案
相关题目
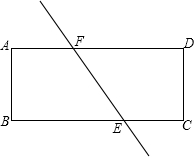 如图是一张矩形纸片ABCD,E,F分别是BC,AD上的点,(但不与顶点重合),如果直线EF将矩形分成面积相等的两部分;
如图是一张矩形纸片ABCD,E,F分别是BC,AD上的点,(但不与顶点重合),如果直线EF将矩形分成面积相等的两部分;  如图,AB是⊙O的弦,半径OD⊥AB于E,AB=24cm,AD=13cm,则OD=$\frac{169}{10}$cm.
如图,AB是⊙O的弦,半径OD⊥AB于E,AB=24cm,AD=13cm,则OD=$\frac{169}{10}$cm.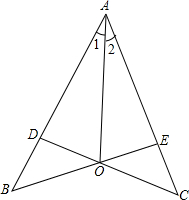 如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.