题目内容
17.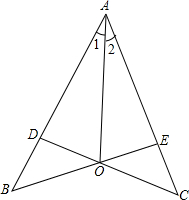 如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
分析 根据AAS证明△ADC与△AEB全等,得出AD=AE,AB=AC,进而得出BD=CE,再根据AAS证明△BDO与△CEO全等,得出OD=OE,利用SAS证明△ADO与△AEO全等即可.
解答 证明:∵∠BEC=∠BDC,
∴∴∠ADC=∠AEB,
在△ADC与△AEB中,
$\left\{\begin{array}{l}{∠ADC=∠AEB}\\{∠BAE=∠DAC}\\{BE=CD}\end{array}\right.$,
∴AD=AE,AB=AC,
∴BD=CE,
在△BDO与△CEO中,
$\left\{\begin{array}{l}{∠BDC=∠CEB}\\{∠DOB=∠EOC}\\{BD=CE}\end{array}\right.$,
∴△BDO≌△CEO(AAS),
∴OD=OE,
在△ADO与△AEO中,
$\left\{\begin{array}{l}{AD=AE}\\{∠ADC=∠AEB}\\{OD=OE}\end{array}\right.$,
∴△ADO≌△AEO(SAS),
∴∠1=∠2.
点评 此题主要考查了全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

练习册系列答案
相关题目
12.若m为大于1的正整数.则多项式xm-1+xm+1+2m+5的次数应当是( )
| A. | m-1 | B. | m+1 | C. | m+5 | D. | 不能确定 |
6.下列代数式的意义叙述中错误的是( )
| A. | x-3y的意义是x与3y的差 | B. | $\frac{4b}{a}$的意义是4b除以a的商 | ||
| C. | (a+b)2的意义是a与b的立方和 | D. | $\frac{2}{3}$(x+y)的意义是x与y的和的$\frac{2}{3}$ |
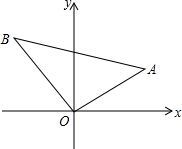 如图,△OAB是等腰直角三角形,AB=4,OA与x轴的夹角为30°,求A、B两点的坐标.
如图,△OAB是等腰直角三角形,AB=4,OA与x轴的夹角为30°,求A、B两点的坐标. 如图,在Rt△ABC中,∠ACB=90°,∠B=2∠A,CD是△ABC的中线,求证:△BCD是等边三角形.
如图,在Rt△ABC中,∠ACB=90°,∠B=2∠A,CD是△ABC的中线,求证:△BCD是等边三角形.