题目内容
19.先化简,再求值:(x+y)2+(y-x)(-y-x),其中|x-$\frac{1}{2}$|+(y+$\frac{1}{3}$)2=0.分析 原式利用完全平方公式及平方差公式化简,去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:∵|x-$\frac{1}{2}$|+(y+$\frac{1}{3}$)2=0,
∴x=$\frac{1}{2}$,y=-$\frac{1}{3}$,
则原式=x2+2xy+y2+x2-y2=2x2+2xy=$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$.
点评 此题考查了整式的混合运算-化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
14.不改变5a2-b2-b+a+ab的值,把二次项放在前面有“+”号的括号里.一次项放在前面有“-”号的括号里,下列各式正确的是( )
| A. | +(5a2+b2+ab)-(b+a) | B. | +(-5a2-b2-ab)-(b-a) | C. | +(5a2-b2+ab)-(b-a) | D. | +(5a2+b2+ab)-(b-a) |
 如图,△ABC、△CDE都是等边三角形
如图,△ABC、△CDE都是等边三角形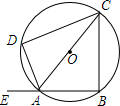 如图,在⊙O中,弦AB的长等于半径,点E在BA的延长线上,∠DAE=80°,则∠ACD=50°.
如图,在⊙O中,弦AB的长等于半径,点E在BA的延长线上,∠DAE=80°,则∠ACD=50°.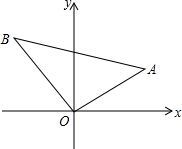 如图,△OAB是等腰直角三角形,AB=4,OA与x轴的夹角为30°,求A、B两点的坐标.
如图,△OAB是等腰直角三角形,AB=4,OA与x轴的夹角为30°,求A、B两点的坐标.