题目内容
15. 如图,AB是⊙O的弦,半径OD⊥AB于E,AB=24cm,AD=13cm,则OD=$\frac{169}{10}$cm.
如图,AB是⊙O的弦,半径OD⊥AB于E,AB=24cm,AD=13cm,则OD=$\frac{169}{10}$cm.
分析 连接OA,先根据垂径定理求出AE的长,再由勾股定理求出DE的长,设OD=r,则OE=r-DE,在Rt△AOE中,根据勾股定理可求出r的值.
解答  解:连接OA,
解:连接OA,
∵OD⊥AB于E,AB=24cm,
∴AE=$\frac{1}{2}$AB=12cm.
∵AD=13cm,
∴DE=$\sqrt{{AD}^{2}-{AE}^{2}}$=$\sqrt{{13}^{2}-{12}^{2}}$=5cm.
设OD=r,则OE=r-DE=(r-5)cm,
在Rt△AOE中,
∵AE2+OE2=OA2,即122+(r-5)2=r2,解得r=$\frac{169}{10}$cm,即OD=$\frac{169}{10}$cm.
故答案为:$\frac{169}{10}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
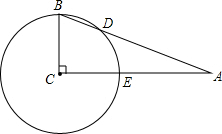 如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E. 如图,△ABC、△CDE都是等边三角形
如图,△ABC、△CDE都是等边三角形 如图,在Rt△ABC中,∠ACB=90°,∠B=2∠A,CD是△ABC的中线,求证:△BCD是等边三角形.
如图,在Rt△ABC中,∠ACB=90°,∠B=2∠A,CD是△ABC的中线,求证:△BCD是等边三角形.