题目内容
17.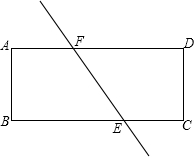 如图是一张矩形纸片ABCD,E,F分别是BC,AD上的点,(但不与顶点重合),如果直线EF将矩形分成面积相等的两部分;
如图是一张矩形纸片ABCD,E,F分别是BC,AD上的点,(但不与顶点重合),如果直线EF将矩形分成面积相等的两部分; (1)问得到的两个四边形是否相似?若相似,请求出类似比;若不相似,请说明理由.
(2)这样的直线可以作几条?
分析 (1)由矩形的性质得出AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,∠AFE=∠CEF,∠BEF=∠DFE,由两个梯形的面积相等得出AF=EC,得出BE=DF,得出两个四边形四条边成比例,由相似多边形的判定方法即可得出结论;
(2)由矩形是中心对称图形得出EF一定经过矩形的对称中心,即可得出结果.
解答 解:(1)得到的两个四边形相似;理由如下:
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,AD∥BC,
∴∠AFE=∠CEF,∠BEF=∠DFE,
∵S梯形ABEF=S梯形CDFE,
∴$\frac{1}{2}$AB(BE+AF)=$\frac{1}{2}$CD(EC+DF),
∴BE+AF=EC+DF,
即BE+AF=EC+AD-AF,
∴2AF=EC+BC-BE=2EC,
∴AF=EC,
∴BE=DF,
∴$\frac{AB}{CD}=\frac{BE}{DF}=\frac{EF}{FE}=\frac{AF}{EC}$,
又∵∠A=∠B=∠C=∠D=90°,∠AFE=∠CEF,∠BEF=∠DFE,
∴四边形ABEF∽四边形CDFE;
(2)∵直线EF将矩形分成面积相等的两部分,
∴EF一定经过矩形的对称中心,
∴这样的直线可以作无数条.
点评 本题考查了矩形的性质、相似多边形的判定方法;熟练掌握矩形的性质,证明两个四边形四条边成比例得出相似是解决问题的关键.

练习册系列答案
相关题目
 探究:我们把过(1,0)且平行于y轴的直线记为x=1,那么过(0,-1)且平行于x轴的直线则记为x=-1;
探究:我们把过(1,0)且平行于y轴的直线记为x=1,那么过(0,-1)且平行于x轴的直线则记为x=-1;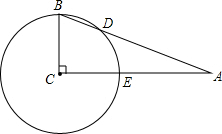 如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
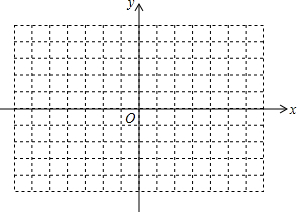
如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫作格点,以格点为顶点按下列要求画三角形.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫作格点,以格点为顶点按下列要求画三角形.