题目内容
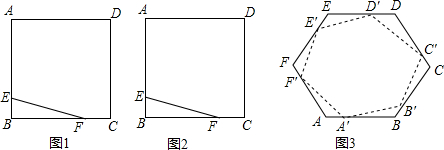
18.已知:如图正方形ABCD中,点E、F分别是边AB和BC上的点,且满足BE=CF.(1)不用圆规,请只用不带刻度的直尺作图:在边CD和DA上分别作出点G和点H,使DG=AH=BE=CF(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,当点E在AB边上的何处时,能使S四边形EFGH:S四边形ABCD=5:8,并说明理由.
(3)如图:正六边形ABCDEF中,点A′、B′、C′、D′、E′、F′分别是边AB、BC、CD、DE、EF、FA上的点,且AA′=BB′=CC′=DD′=EE′=FF′.
①设AA′:A′B=1:3,则S六边形A′B′C′D′E′F′:S六边形ABCDEF=13:16
②设AA′:A′B=k,求S六边形A′B′C′D′E′F′:S六边形ABCDEF的值(用含k的代数式表示).
分析 (1)根据正方形是中心对称图形作图即可;
(2)设BE=CF=x,根据勾股定理表示出EF,根据相似多边形的性质列出比例式,计算即可;
(3)①作B′H⊥AB交AB的延长线于H,设AA′=a,根据题意表示出A′B,利用三角函数的定义表示出B′H和BH,根据勾股定理求出A′B′,根据相似多边形的性质计算即可;
②设AA′=k,利用①的思路进行解答即可.
解答 解: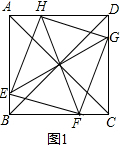 (1)如图1所示:DG=AH=BE=CF;
(1)如图1所示:DG=AH=BE=CF;
(2)设BE=CF=x,BC=y,则BF=y-x,
由勾股定理得,EF2=BE2+BF2=x2+(y-x)2=2x2-2xy+y2,
∵S四边形EFGH:S四边形ABCD=5:8,
∴(2x2-2xy+y2):(y2)=5:8,
则2($\frac{x}{y}$)2-2×$\frac{x}{y}$+$\frac{3}{8}$=0,
解得,$\frac{x}{y}$=$\frac{1}{4}$,$\frac{x}{y}$=$\frac{3}{4}$,
∴当BE=$\frac{1}{4}$AB或BE=$\frac{3}{4}$AB时,S四边形EFGH:S四边形ABCD=5:8;
(3)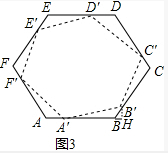 ①如图3,作B′H⊥AB交AB的延长线于H,
①如图3,作B′H⊥AB交AB的延长线于H,
设AA′=a,则A′B=3a,AB=4a,B′B=a,
∵六边形ABCDEF为正六边形,
∴∠ABC=120°,
∴∠B′BH=60°,
∴BH=$\frac{1}{2}$a,B′H=$\frac{\sqrt{3}}{2}$a,
∴A′B′=$\sqrt{A′{H}^{2}+B′{H}^{2}}$=$\sqrt{13}$a,
∴$\frac{A′B′}{AB}$=$\frac{\sqrt{13}}{4}$,
∴S六边形A′B′C′D′E′F′:S六边形ABCDEF=13:16,
故答案为:13:16;
②∵AA′:A′B=k,
∴设AA′=k,则A′B=1,
则BH=$\frac{1}{2}$k,B′H=$\frac{\sqrt{3}}{2}$k,
∴A′B′=$\sqrt{A′{H}^{2}+B′{H}^{2}}$=$\sqrt{1+k+{k}^{2}}$,
AB=1+k,
∴S六边形A′B′C′D′E′F′:S六边形ABCDEF=($\frac{A′B′}{AB}$)2=$\frac{1+k+{k}^{2}}{1+2k+{k}^{2}}$.
点评 本题考查的是正方形和正六边形的性质以及全等三角形的判定和性质,掌握正方形是中心对称图形、正确求出正六边形的内角的度数、熟记锐角三角函数的定义是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y2-3y+2=0 | B. | y2-3y-2=0 | C. | y2+3y+2=0 | D. | y2+3y-2=0 |
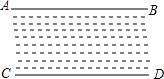 如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.
如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.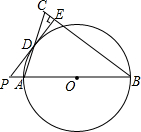 如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.
如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.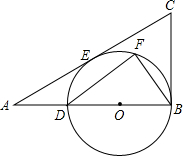 如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.
如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.