题目内容
9.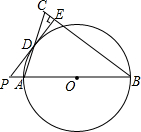 如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.
如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.(1)判断直线PE与⊙O的位置关系,并说明理由;
(2)若PA=1,∠B=30°,求⊙O的半径.
分析 (1)连结OD,如图,根据等腰三角形的性质得∠1=∠C,∠1=∠2,则∠2=∠C,于是可判断OD∥BC,再利用PE⊥BC可得PE⊥OD,然后根据切线的判定定理得到结论;
(2)设⊙O的半径为r,根据平行线的性质得∠POD=∠B=30°,然后利用余弦定义得到即$\frac{\sqrt{3}}{2}$=$\frac{r}{r+1}$,再解方程求出r即可.
解答 解:(1)直线PE与⊙O相切.理由如下:
连结OD,如图,
∵AB=CB,
∴∠1=∠C,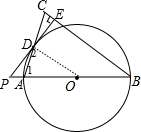
∵OD=OA,
∴∠1=∠2,
∴∠2=∠C,
∴OD∥BC,
∵PE⊥BC,
∴PE⊥OD,
∴直线PE为⊙O的切线;
(2)设⊙O的半径为r,
∵OD∥BC,
∴∠POD=∠B=30°,
在Rt△POD中,cos∠POD=$\frac{OD}{OP}$,
即$\frac{\sqrt{3}}{2}$=$\frac{r}{r+1}$,解得r=2$\sqrt{3}$+3,
即⊙O的半径为2$\sqrt{3}$+3.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.解决(1)小题的关键是证明OD∥BC.

练习册系列答案
相关题目
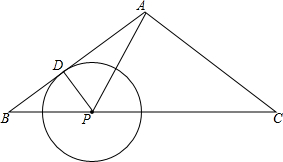 如图,在△ABC中,AB=AC=10,BC=16,点P为BC边上的一个动点,以P为圆心的⊙P与边AB相切于点D.在点P移动的过程中,△APC如果成为等腰三角形,求⊙P的半径.
如图,在△ABC中,AB=AC=10,BC=16,点P为BC边上的一个动点,以P为圆心的⊙P与边AB相切于点D.在点P移动的过程中,△APC如果成为等腰三角形,求⊙P的半径.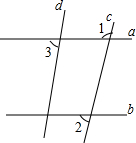 如图,已知∠1=98°,∠2=∠3=82°,试说明:a∥b,c∥d.
如图,已知∠1=98°,∠2=∠3=82°,试说明:a∥b,c∥d.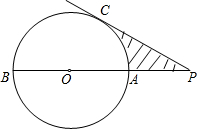 如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).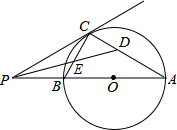 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.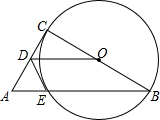 如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
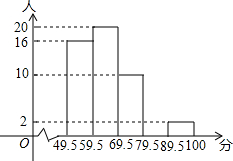 某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:
某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组: