题目内容
6.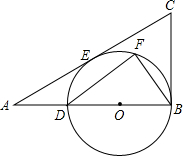 如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.
如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.(1)求0B的长;
(2)过点D作DF∥AC交⊙O于点F,连结BF,求△DFB的周长.
分析 (1)要求OB的长,只要求的⊙O的半径即可,根据在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,AD=4,作辅助线连接OE,则∠AEO=90°,可以求得OE的长,本题得以解决;
(2)根据DF∥AC,可以得到∠EDB=∠A,然后根据第一问求得的OB的长和tanA=$\frac{3}{4}$,可以分别求得△DFB的各边的长,从而可以求得△DFB的周长.
解答 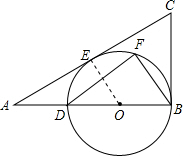 解:(1)连接OE,如右图所示,
解:(1)连接OE,如右图所示,
∵以BD为直径的⊙O与边AC切于点E,
∴∠AEO=90°,
∵$tanA=\frac{3}{4},tanA=\frac{OE}{AE}$,
∴设OE=3a,AE=4a,则AO=$\sqrt{(3a)^{2}+(4a)^{2}}=5a$,
又∵AO=AD+DO,AD=4,DO=OE,
∴5a=4+3a,
解得,a=2,
∴3a=6,
即OE=6,
∵OB=OE,
∴OB=6;
(2)∵BD为⊙O的直径,DF∥AC,tanA=$\frac{3}{4}$,
∴∠DFB=90°,∠FDB=∠A,BD=2OE=12,
∴tan∠FDB=$\frac{3}{4}$,
设BF=3x,DF=4x,
∴122=(3x)2+(4x)2
解得x=2.4,
∴3x=7.2,4x=9.6,
∴△DFB的周长是:7.2+9.6+12=28.8,
即△DFB的周长是28.8.
点评 本题考查切线的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若一个多边形的每个内角都是120°,这个多边形是( )
| A. | 八角形 | B. | 七边形 | C. | 五边形 | D. | 六边形 |
15.在学校乒乓球比赛中,从陈亮、李明、刘松、周杰、王刚这五人中,随机抽签一组对手,正好抽到王刚与刘松的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
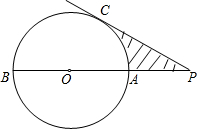 如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).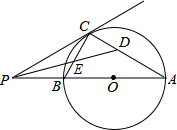 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.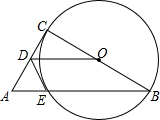 如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
 如图,在每个小正方形边长为1的网格纸中,将格点△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,在每个小正方形边长为1的网格纸中,将格点△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.