题目内容
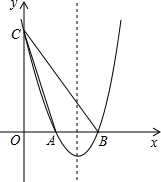 如图,已知二次函数y=a(x2-6x+8)(a>0)的图象与x轴交于点A、B两点,与y轴交于点C.
如图,已知二次函数y=a(x2-6x+8)(a>0)的图象与x轴交于点A、B两点,与y轴交于点C.(1)求A、B两点的坐标;
(2)将△OAC沿直线AC翻折,点O的对应点为O′.
①若O'落在该抛物线的对称轴上,求实数a的值;
②是否存在正整数a,使得点O′落在△ABC的内部?若存在,求出整数a的值;若不存在,请说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)令y=0,解关于x的方程即可得到点A、B的坐标;
(2)①设对称轴与x轴的交点为E,求出AE=1,再根据翻折变换的性质可得AO′=AO,然后利用∠O′AE的余弦值求出角的度数,再求出∠CAO=60°,然后利用∠CAO的正切值列式计算即可得解;
③过点A作AF⊥BC于F,根据垂线段最短可得AF<AB,再根据翻折变换的性质可得AO′=AO=2,从而判断出点O′总落在△ABC的外部.
(2)①设对称轴与x轴的交点为E,求出AE=1,再根据翻折变换的性质可得AO′=AO,然后利用∠O′AE的余弦值求出角的度数,再求出∠CAO=60°,然后利用∠CAO的正切值列式计算即可得解;
③过点A作AF⊥BC于F,根据垂线段最短可得AF<AB,再根据翻折变换的性质可得AO′=AO=2,从而判断出点O′总落在△ABC的外部.
解答:解:(1)令y=0,则x2-6x+8=0,
解得x1=2,x2=4,
所以,A(2,0),B(4,0);

(2)①如图,抛物线的对称轴为直线x=-
=3,
设对称轴与x轴的交点为E,求出AE=1,
将△OAC沿直线AC翻折,点O的对应点O′落在对称轴x=3上,
∵A(2,0),
∴AO=2,
在Rt△O′AE中,cos∠O′AM=
=
,
∴∠O′AM=60°,
∴∠CAO=
×(180°-∠O′AM)=
×(180°-60°)=60°,
∴tan∠CAO=
=
=
,
解得a=
;
②过A点作AF⊥BC,F为垂足,
由垂线段最短可得AF<AB=2,
由翻折的性质得,AO′=AO=2,
所以,不论a取何值,O点的对应点O′总落在△ABC的外部,
所以,这样的整数a不存在.
解得x1=2,x2=4,
所以,A(2,0),B(4,0);

(2)①如图,抛物线的对称轴为直线x=-
| -6 |
| 2×1 |
设对称轴与x轴的交点为E,求出AE=1,
将△OAC沿直线AC翻折,点O的对应点O′落在对称轴x=3上,
∵A(2,0),
∴AO=2,
在Rt△O′AE中,cos∠O′AM=
| AE |
| AO′ |
| 1 |
| 2 |
∴∠O′AM=60°,

∴∠CAO=
| 1 |
| 2 |
| 1 |
| 2 |
∴tan∠CAO=
| OC |
| OA |
| 8a |
| 2 |
| 3 |
解得a=
| ||
| 4 |
②过A点作AF⊥BC,F为垂足,
由垂线段最短可得AF<AB=2,
由翻折的性质得,AO′=AO=2,
所以,不论a取何值,O点的对应点O′总落在△ABC的外部,
所以,这样的整数a不存在.
点评:本题是二次函数综合题型,主要利用了二次函数与x轴的交点的求解,翻折变换的性质,锐角三角函数的定义,垂线段最短的性质,综合题,但难度不大,熟记各性质是解题的关键.

练习册系列答案
相关题目
如果一个正比例函数的图象经过不同象限的两点A(5,m),B(n,8),那么一定有( )
| A、m>0,n>0 |
| B、m>0,n<0 |
| C、m<0,n>0 |
| D、m<0,n<0 |
 如图,B、C为线段AB上的两点,且AB=
如图,B、C为线段AB上的两点,且AB= 如图,已知,如图,BCE,AFE是直线,AD∥BC,∠1=∠2,∠3=∠4,求证:AB∥CD.
如图,已知,如图,BCE,AFE是直线,AD∥BC,∠1=∠2,∠3=∠4,求证:AB∥CD.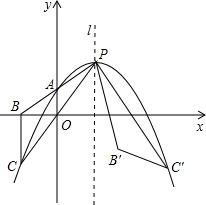 如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.