题目内容
因式分解：
（1）a2（x-y）-b2（x-y）；
（2）4a2b2-4a3b-ab3．
（1）a2（x-y）-b2（x-y）；
（2）4a2b2-4a3b-ab3．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）首先提取公因式（x-y），进而利用平方差公式分解因式即可；
（2）首先提取公因式-ab，进而利用完全平方公式分解因式即可．
（2）首先提取公因式-ab，进而利用完全平方公式分解因式即可．
解答：解：（1）原式=（x-y）（a2-b2）=（x-y）（a+b）（a-b）；
（2）原式=-ab（4a2-4ab+b2）=-ab（2a-b）2．
（2）原式=-ab（4a2-4ab+b2）=-ab（2a-b）2．
点评：此题主要考查了提取公因式法以及公式法分解因式，熟练应用乘法公式是解题关键．
练习册系列答案
相关题目
设max表示两个数中的最大值，倒如max{0，2}=2，max{12，8}=12，则关于x的函数y=max{3x，2x+1}可表示为（ ）
| A、y=3x | |||||
| B、y=2x+1 | |||||
C、y=
| |||||
D、y=
|
如果a＞b，则下列式子错误的是（ ）
| A、a+2＞b+2 | ||||
| B、a-2＞b-2 | ||||
| C、2a＞2b | ||||
D、-
|
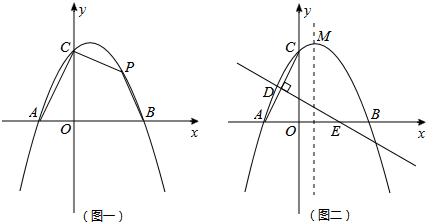
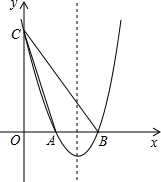如图，已知二次函数y=a（x2-6x+8）（a＞0）的图象与x轴交于点A、B两点，与y轴交于点C．
如图，在⊙A中，试列举出一条直径、两条半径、三条弦、三段弧、三个圆周角、三个圆心角．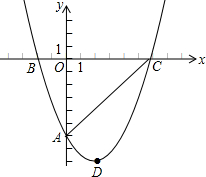
如图，经过点A（0，-6）的抛物线y=