题目内容
18.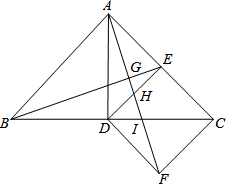 如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.(1)求证:AF⊥BE;
(2)求证:AD=3DI.
分析 (1)根据翻折的性质和SAS证明△ABE与△ACF全等,利用全等三角形的性质得出∠AGB=90°证明即可;
(2)作IC的中点M,利用AAS证明△AEH与△FDH全等,再利用全等三角形的性质和中位线的性质解答即可.
解答 证明:(1)∵在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,∠ACB=45°,
∵在△ADC中,AD=DC,DE⊥AC,
∴AE=CE,
∵△CDE沿直线BC翻折到△CDF,
∴△CDE≌△CDF,
∴CF=CE,∠DCF=∠ACB=45°,
∴CF=AE,∠ACF=∠DCF+∠ACB=90°,
在△ABE与△ACF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠ACF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△ACF(SAS),
∴∠ABE=∠FAC,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE;
(2)作IC的中点M,连接EM,由(1)∠DEC=∠ECF=∠CFD=90°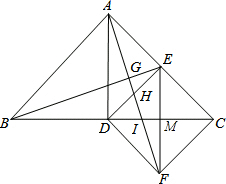
∴四边形DECF是正方形,
∴EC∥DF,EC=DF,
∴∠EAH=∠HFD,AE=DF,
在△AEH与△FDH中$\left\{\begin{array}{l}{∠AHE=∠DHF}\\{∠EAH=∠HFD}\\{AE=DF}\end{array}\right.$,
∴△AEH≌△FDH(AAS),
∴EH=DH,
∵∠BAG+∠CAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∵M是IC的中点,E是AC的中点,
∴EM∥AI,
∴$\frac{DI}{TM}=\frac{DH}{HE}=1$,
∴DI=IM,
∴CD=DI+IM+MC=3DI,
∴AD=3DI.
点评 此题考查翻折问题,关键是利用SAS和AAS证明三角形全等,再利用全等三角形的性质进行分析解答.

| A. | 3$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 18$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
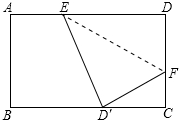 如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
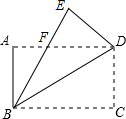 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间. 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( ) 如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.
如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.