题目内容
13.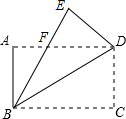 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.(1)求证:△EDF≌△ABF;
(2)∠ABF=30°,AB=2$\sqrt{3}$,求△BDF的面积.
分析 (1)因为四边形ABCD是矩形,折叠前后∠E=∠C=90°,ED=CD=AB,所以根据AAS可证;
(2)要想求出△BDF的面积,根据题中条件,只要求出△AFB或者△FDE面积后,利用求差的办法即可求得△BDF的面积.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,
由折叠可得,∠E=∠C=90°,ED=CD,
在△ABF和△EDF中,
$\left\{\begin{array}{l}{∠AFB=∠EFD}\\{∠A=∠E}\\{AB=ED}\end{array}\right.$,
∴△ABF≌△EDF(AAS);
(2)在Rt△ABF中,∠A=90°,∠ABF=30°,
∴AF=$\frac{1}{2}$BF,
∵AB=2$\sqrt{3}$,
由勾股定理得,BF2-($\frac{1}{2}$BF)2=(2$\sqrt{3}$)2,
∴BF=4,
∴DF=4,
∴S△BDF=$\frac{1}{2}×4×2\sqrt{3}$=4$\sqrt{3}$.
点评 本题综合考查图形的折叠问题,勾股定理的应用以及三角形面积求法,折叠问题注意图形折叠前后对应边相等,对应角相等,此题难度不大.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
16.已知⊙O的半径为5,直线l是⊙O的切线,则点O到直线l的距离是( )
| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |

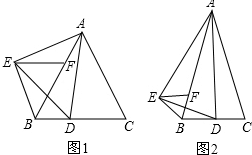
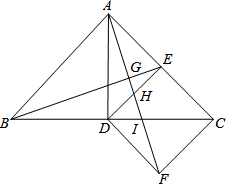 如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.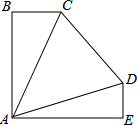 将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.
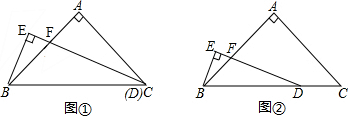
将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.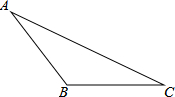 如图,在△ABC中画出高线AD、中线BE、角平分线CF.
如图,在△ABC中画出高线AD、中线BE、角平分线CF.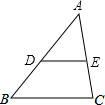 如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE$\stackrel{∥}{=}$$\frac{1}{2}$BC.
如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE$\stackrel{∥}{=}$$\frac{1}{2}$BC.