题目内容
2.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+3y=k}\\{x+2y=-1}\end{array}\right.$的解互为相反数,则k的值是-1.分析 将方程组用k表示出x,y,根据方程组的解互为相反数,得到关于k的方程,即可求出k的值.
解答 解:解方程组$\left\{\begin{array}{l}{2x+3y=k}\\{x+2y=-1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=2k+3}\\{y=-2-k}\end{array}\right.$,
因为关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+3y=k}\\{x+2y=-1}\end{array}\right.$的解互为相反数,
可得:2k+3-2-k=0,
解得:k=-1.
故答案为:-1.
点评 此题考查方程组的解,关键是用k表示出x,y的值.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a2•a3=a6 | C. | (-a2)2=a4 | D. | (a+1)2=a2+1 |
13. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )
 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
7.为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
| 目的地 车型 | A村(元/辆) | B村(元/辆) |
| 大货车 | 800 | 900 |
| 小货车 | 400 | 600 |
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
19.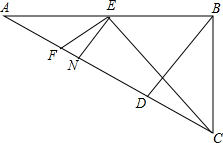 如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
 如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |

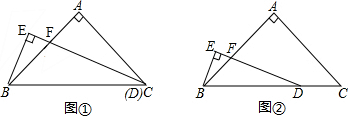
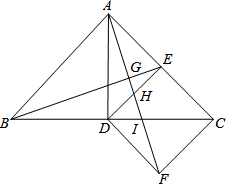 如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.