题目内容
1.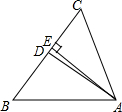 在△ABC中,∠B=50°,∠C=56°,AD平分∠CAB,AE⊥BC于E,求∠DAE的度数.
在△ABC中,∠B=50°,∠C=56°,AD平分∠CAB,AE⊥BC于E,求∠DAE的度数.
分析 首先根据三角形的内角和定理,求出∠CAB的度数是多少;然后根据AD平分∠CAB,求出∠CAD的度数是多少;最后根据AE⊥BC,求出∠CAE的度数,再用∠CAD的度数减去∠CAE的度数,求出∠DAE的度数是多少即可.
解答 解:∵∠B+∠C+∠CAB=180°,
∴∠CAB=180°-50°-56°=74°,
∵AD平分∠CAB,
∴∠CAD=74÷2=37°,
∵AE⊥BC,
∴∠CAE=90°-∠C=90°-56°=34°,
∴∠DAE=∠CAD-∠CAE=37°-34°=3°,
即∠DAE的度数是3°.
点评 (1)此题主要考查了三角形的内角和定理的应用,要熟练掌握,解答此题的关键是要明确:三角形内角和是180°.
(2)此题还考查了三角形的角平分线的性质的应用,以及直角三角形的性质的应用,要熟练掌握.

练习册系列答案
相关题目
12.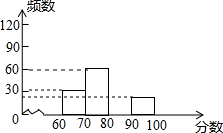 “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
请根据以上图表提供的信息,解答下列问题:
(1)表中m的值为200,n的值为0.3;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
 “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:| 分段数 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 60 | n |
| 80≤x<90 | ||
| 90≤x<100 | 20 | 0.1 |
| 合计 | m | 1 |
(1)表中m的值为200,n的值为0.3;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
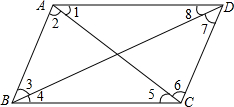 如图,在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中,内错角有几对,它们分别是哪两条直线被哪两条直线所截而构成的?
如图,在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中,内错角有几对,它们分别是哪两条直线被哪两条直线所截而构成的?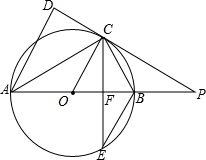 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,连接BE
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,连接BE