题目内容
16．已知$\frac{2a+2b}{a-b}$=$\frac{1}{3}$，则$\frac{a}{b}$=-$\frac{7}{5}$；$\frac{2a}{3b}$=-$\frac{14}{15}$．分析 根据比例的性质进行解答即可．
解答 解：因为$\frac{2a+2b}{a-b}$=$\frac{1}{3}$，
可得：6a+6b=a-b，
即可得：5a=-7b，
所以$\frac{a}{b}=-\frac{7}{5}$，$\frac{2a}{3b}=-\frac{2}{3}×\frac{7}{5}=-\frac{14}{15}$，
故答案为：$-\frac{7}{5}$；-$\frac{14}{15}$．
点评 此题考查比例的性质，关键是利用比例的性质得出5a=-7b，代入解答即可．
练习册系列答案
应用题作业本系列答案
相关题目
如图，为测量某楼AB的高度，工作人员在点D处高1.8m的测角仪CD测得楼顶端A的仰角为30°，向前走40m到点E，又测得点A的仰角为60°，求楼AB的高度．（最后结果取近似值，保留两位小数，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
4．某校七年级“启航班”的同学在老师带领下学习“数学活动”，步骤如下：
（1）将全班同学分成几组，每组三人，合作完成本次数学活动．
（2）每三人小组分别测试1分钟跳绳的次数并对照得分表换算成得分．
（3）老师从中抽查了一个小组甲、乙、丙同学的得分数据，让同学们绘制成折线统计图．
（4）根据折线统计图（图1）填写下表：
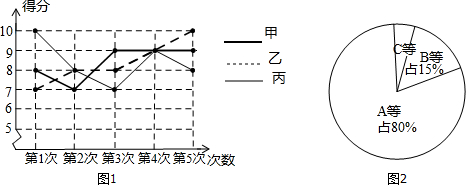
（5）用测试统计的数据制成扇形统计图（图2）可知：跳绳成绩A等的学生占80%，在扇形图中所占圆心角为288度，B等的学生占15%，C等的学生有2人，占5%，参加跳绳的学生共有40人．
（1）将全班同学分成几组，每组三人，合作完成本次数学活动．
（2）每三人小组分别测试1分钟跳绳的次数并对照得分表换算成得分．
（3）老师从中抽查了一个小组甲、乙、丙同学的得分数据，让同学们绘制成折线统计图．
（4）根据折线统计图（图1）填写下表：
| 平均数 | 众 数 | 中位数 | 方 差 | 综合评价 | |
| 甲 | 8.4 | 9 | 9 | 0.64 | 成绩较为稳定的学生是甲． |
| 乙 | 8.4 | 8 | 8 | 1.04 | |
| 丙 | 8.4 | 8 | 1.04 |
11．
如图，BD是⊙O的直径，弦AC⊥BD，垂足为E，∠AOB=60°，则∠BDC等于（ ）
如图，BD是⊙O的直径，弦AC⊥BD，垂足为E，∠AOB=60°，则∠BDC等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
在△ABC中，∠B=50°，∠C=56°，AD平分∠CAB，AE⊥BC于E，求∠DAE的度数．
一艘巡逻艇从小岛B出发，沿北偏西75°方向航行10（$\sqrt{3}$+1）海里到达A处时，收到由小岛B处求救中心发给它的指令，要求该巡逻艇30分钟内赶到海上C处进行救援，此时C处位于B处南偏西60°，位于巡逻艇南偏东45°，接到指令后巡逻艇立即以每小时50海里的速度赶往C处，问：巡逻艇能否在规定时间内赶到？
如下：已知CA=CB，那么数轴上点A所表示的数是1$-\sqrt{10}$．