题目内容
12.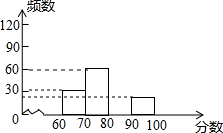 “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:| 分段数 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 60 | n |
| 80≤x<90 | ||
| 90≤x<100 | 20 | 0.1 |
| 合计 | m | 1 |
(1)表中m的值为200,n的值为0.3;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
分析 (1)用60≤x<70的频数和频率先求出总人数,再根据$\frac{频数}{总数}$=频率求出n的值即可;
(2)先求出80≤x<90的频数,再画图即可;
(3)根据中位数的定义找出第100、101个数所在的分数段即可;
(4)用全校的总人数乘以试成绩80分以上(含80分)的人数所占的比即可.
解答 解:(1)根据题意得:m=$\frac{30}{0.15}$=200(名),
n=$\frac{60}{200}$=0.3;
故答案为:200,0.3;
(2)80≤x<90的人数是:200-30-60-20=90(人),补图如下: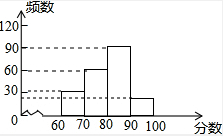
(3)因为共有200人,则中位数是100,101个数的平均数,
所以测试成绩的中位数在80≤x<90分数段;
(4)根据题意得:
1200×$\frac{90+20}{200}$=660(人),
答:全校学生中合格人数约为660人.
点评 本题考查了频数分布直方图,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题;本题用到的知识点是:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数;频率=频数÷总数,用样本估计整体让整体×样本的百分比.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
4.某校七年级“启航班”的同学在老师带领下学习“数学活动”,步骤如下:
(1)将全班同学分成几组,每组三人,合作完成本次数学活动.
(2)每三人小组分别测试1分钟跳绳的次数并对照得分表换算成得分.
(3)老师从中抽查了一个小组甲、乙、丙同学的得分数据,让同学们绘制成折线统计图.
(4)根据折线统计图(图1)填写下表:
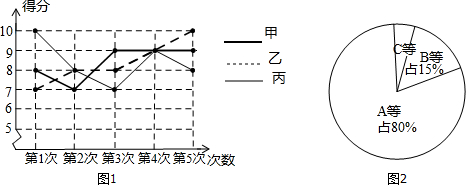
(5)用测试统计的数据制成扇形统计图(图2)可知:跳绳成绩A等的学生占80%,在扇形图中所占圆心角为288度,B等的学生占15%,C等的学生有2人,占5%,参加跳绳的学生共有40人.
(1)将全班同学分成几组,每组三人,合作完成本次数学活动.
(2)每三人小组分别测试1分钟跳绳的次数并对照得分表换算成得分.
(3)老师从中抽查了一个小组甲、乙、丙同学的得分数据,让同学们绘制成折线统计图.
(4)根据折线统计图(图1)填写下表:

| 平均数 | 众 数 | 中位数 | 方 差 | 综合评价 | |
| 甲 | 8.4 | 9 | 9 | 0.64 | 成绩较为稳定的学生是甲. |
| 乙 | 8.4 | 8 | 8 | 1.04 | |
| 丙 | 8.4 | 8 | 1.04 |
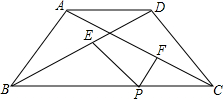 如图,在等腰梯形ABCD中,AD∥BC,AB=CD=3,P是BC上一点,PE∥CD交BD于点E,PF∥AB交AC于点F,设PE、PF的长分别是m、n,且x=m+n,那么当P在BC上移动时,x的值是否变化?若变化,求出x的取值范围;若不变,求出x的值.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD=3,P是BC上一点,PE∥CD交BD于点E,PF∥AB交AC于点F,设PE、PF的长分别是m、n,且x=m+n,那么当P在BC上移动时,x的值是否变化?若变化,求出x的取值范围;若不变,求出x的值.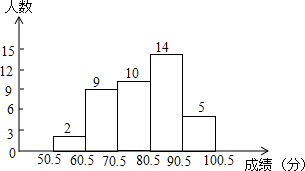 初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:
初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题: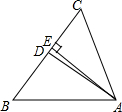 在△ABC中,∠B=50°,∠C=56°,AD平分∠CAB,AE⊥BC于E,求∠DAE的度数.
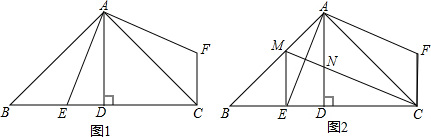
在△ABC中,∠B=50°,∠C=56°,AD平分∠CAB,AE⊥BC于E,求∠DAE的度数. 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2$\sqrt{2}$,BM=1,则MN的长为$\frac{5}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2$\sqrt{2}$,BM=1,则MN的长为$\frac{5}{3}$.