题目内容
10.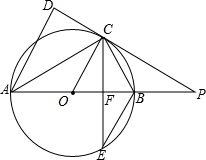 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,连接BE
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,连接BE(1)求证:PD是⊙O的切线;
(2)若tan∠ABC=$\frac{4}{3}$,BE=7$\sqrt{2}$,求线段PC的长.
分析 (1)由AC平分∠DAB得∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,由于AD⊥DC,所以OC⊥DC,则可根据切线的判定定理得到PD是⊙O的切线;
(2)连结AE,如图,根据圆周角定理得到∠ACB=90°,则∠ACE=∠BCE=45°,所以∠ABE=∠ACE=∠BAE=∠BCE=45°,则可判断△AEB为等腰直角三角形,所以AB=$\sqrt{2}$BE=14,在Rt△ACB中利用正切定义设AC=4x,BC=3x,则AB=5x,所以5x=14,解得x=$\frac{14}{5}$,则AC=$\frac{56}{5}$,BC=$\frac{42}{5}$,接着证明Rt△ACD∽Rt△ABC,利用相似比计算出AD=$\frac{224}{25}$,CD=$\frac{168}{25}$,然后证明△POC∽△PAD,利用相似的性质得$\frac{PC}{PC+\frac{168}{25}}$=$\frac{7}{\frac{224}{25}}$,再利用比例性质可计算出PC.
解答 (1)证明:∵AC平分∠DAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥DC,
∴OC⊥DC,
∴PD是⊙O的切线;
(2)解:连结AE,如图,
∵AB为直径,
∴∠ACB=90°,
∵弦CE平分∠ACB,
∴∠ACE=∠BCE=45°,
∴∠ABE=∠ACE=45°,∠BAE=∠BCE=45°,
∴△AEB为等腰直角三角形,
∴AB=$\sqrt{2}$BE=$\sqrt{2}$×7$\sqrt{2}$=14,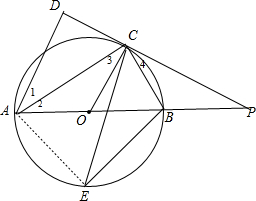
在Rt△ACB中,tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,
设AC=4x,BC=3x,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5x,
∴5x=14,解得x=$\frac{14}{5}$,
∴AC=$\frac{56}{5}$,BC=$\frac{42}{5}$,
∵∠1=∠2,
∴Rt△ACD∽Rt△ABC,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$=$\frac{CD}{BC}$,即$\frac{AD}{\frac{56}{5}}$=$\frac{\frac{56}{5}}{14}$=$\frac{CD}{\frac{42}{5}}$,
∴AD=$\frac{224}{25}$,CD=$\frac{168}{25}$,
∵OC∥AD,
∴△POC∽△PAD,
∴$\frac{PC}{PD}$=$\frac{OC}{AD}$,即$\frac{PC}{PC+\frac{168}{25}}$=$\frac{7}{\frac{224}{25}}$,
∴PC=24.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | x3+x3=x6 | B. | (-a2)3•a6=a12 | C. | (m5)5=m10 | D. | x5y5=(xy)5 |
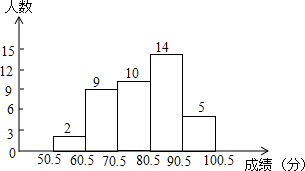 初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:
初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题: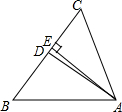 在△ABC中,∠B=50°,∠C=56°,AD平分∠CAB,AE⊥BC于E,求∠DAE的度数.
在△ABC中,∠B=50°,∠C=56°,AD平分∠CAB,AE⊥BC于E,求∠DAE的度数. 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2$\sqrt{2}$,BM=1,则MN的长为$\frac{5}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2$\sqrt{2}$,BM=1,则MN的长为$\frac{5}{3}$.