题目内容
1.丽威办公用品工厂要生产280个书桌,计划用14天完成任务,当生产任务完成到一半时,发现以后只有每天比原来多生产21个书桌,才能恰好用14天完成任务.设原来平均每天生产x个书桌,下面所列方程正确的是( )| A. | $\frac{140}{x}$+$\frac{140}{x-21}$=14 | B. | $\frac{140}{x}$+$\frac{140}{x+21}$=14 | C. | $\frac{280}{x}$+$\frac{280}{x+21}$=14 | D. | $\frac{280}{x}$+$\frac{280}{x-21}$=14 |
分析 先根据工作总量=工作时间×工作效率,用实际天数+计划天数=14列出方程解答即可.
解答 解:设原来平均每天生产x个书桌,可得:$\frac{140}{x}+\frac{140}{x+21}=14$,
故选B
点评 本题考查分式方程的应用,关键是依据工作时间,工作效率以及工作总量之间数量关系解决问题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
12. 如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )
 如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,且CD=CE,∠D=75°,则∠B的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
16.下列运算正确的是( )
| A. | (a2)3=a5 | B. | 2a-2=$\frac{1}{2{a}^{2}}$ | C. | a6÷a2=a3 | D. | (ab2)2=a2b4 |
13.己知⊙O的半径为$\sqrt{2}$,弦AB=2,以AB为底边,在圆内画⊙0的内接等腰△ABC,则底边AB边上的高CD长为( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}+1$或$\sqrt{2}$-1 | D. | $\sqrt{2}$+1或$\sqrt{3}$+1 |
2.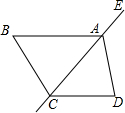 在四边形ABCD中AB∥CD,点E在CA的延长线上,若∠EAB=130°,则下列结论正确的是( )
在四边形ABCD中AB∥CD,点E在CA的延长线上,若∠EAB=130°,则下列结论正确的是( )
 在四边形ABCD中AB∥CD,点E在CA的延长线上,若∠EAB=130°,则下列结论正确的是( )
在四边形ABCD中AB∥CD,点E在CA的延长线上,若∠EAB=130°,则下列结论正确的是( )| A. | ∠ACB=50° | B. | ∠ACD=50° | C. | ∠ADC=130° | D. | ∠EAD=130° |
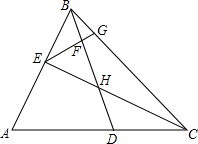 如图,△ABC中,∠A=60°,在AC上截取AD=AB,E为AB上一点,且BE=CD,过点E作BD的垂线,分别交BD、BC于F、G,连接EC交BD于H.
如图,△ABC中,∠A=60°,在AC上截取AD=AB,E为AB上一点,且BE=CD,过点E作BD的垂线,分别交BD、BC于F、G,连接EC交BD于H.