题目内容
13.己知⊙O的半径为$\sqrt{2}$,弦AB=2,以AB为底边,在圆内画⊙0的内接等腰△ABC,则底边AB边上的高CD长为( )| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}+1$或$\sqrt{2}$-1 | D. | $\sqrt{2}$+1或$\sqrt{3}$+1 |
分析 如图1,连接OA,根据垂径定理得到AD=BD,CD过圆心,由勾股定理得到OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=1,于是得到CD=OC+OD=1+$\sqrt{2}$,如图2,连接OA,同理得到CD=OC-OD=$\sqrt{2}$-1.
解答 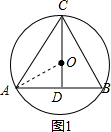 解:如图1,连接OA,
解:如图1,连接OA,
∵AC=BC=$\frac{1}{2}$AB=1,CD⊥AB,
∴AD=BD,CD过圆心,
∴OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=1,
∴CD=OC+OD=1+$\sqrt{2}$,
如图2,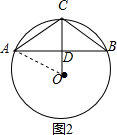 连接OA,
连接OA,
∵AC=BC=$\frac{1}{2}$AB=1,CD⊥AB,
∴AD=BD,CD过圆心,
∴OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=1,
∴CD=OC-OD=$\sqrt{2}$-1,
综上所述:$\sqrt{2}+$1或$\sqrt{2}-$1.
故选C.
点评 本题考查了垂径定理,等腰三角形的性质,勾股定理.正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
1.丽威办公用品工厂要生产280个书桌,计划用14天完成任务,当生产任务完成到一半时,发现以后只有每天比原来多生产21个书桌,才能恰好用14天完成任务.设原来平均每天生产x个书桌,下面所列方程正确的是( )
| A. | $\frac{140}{x}$+$\frac{140}{x-21}$=14 | B. | $\frac{140}{x}$+$\frac{140}{x+21}$=14 | C. | $\frac{280}{x}$+$\frac{280}{x+21}$=14 | D. | $\frac{280}{x}$+$\frac{280}{x-21}$=14 |
 解不等式组$\left\{\begin{array}{l}{3x-2<2x①}\\{\frac{1+x}{2}-1≤x②}\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}{3x-2<2x①}\\{\frac{1+x}{2}-1≤x②}\end{array}\right.$请结合题意填空,完成本题的解答.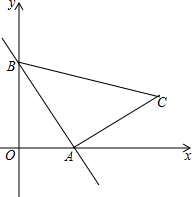 如图,在平面直角坐标系中,点C的坐标为(3,1),动点A以每秒1个单位的速度从点O出发沿x轴正半轴运动,同时动点B以每秒2个单位的速度从点O出发沿y轴正半轴运动,作直线AB.设运动的时间为t秒,是否存在t,使△ABC是等腰三角形?若存在,求t的值;若不存在,请说明理由.
如图,在平面直角坐标系中,点C的坐标为(3,1),动点A以每秒1个单位的速度从点O出发沿x轴正半轴运动,同时动点B以每秒2个单位的速度从点O出发沿y轴正半轴运动,作直线AB.设运动的时间为t秒,是否存在t,使△ABC是等腰三角形?若存在,求t的值;若不存在,请说明理由.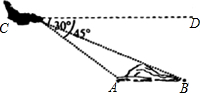 钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73)
钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73) 在正方形ABCD中,点F是对角线AC上任意一点,EF⊥BF交边AD于点E,联结BE.求∠EBF.
在正方形ABCD中,点F是对角线AC上任意一点,EF⊥BF交边AD于点E,联结BE.求∠EBF.