题目内容
1.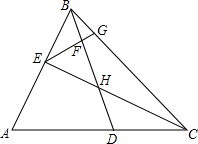 如图,△ABC中,∠A=60°,在AC上截取AD=AB,E为AB上一点,且BE=CD,过点E作BD的垂线,分别交BD、BC于F、G,连接EC交BD于H.
如图,△ABC中,∠A=60°,在AC上截取AD=AB,E为AB上一点,且BE=CD,过点E作BD的垂线,分别交BD、BC于F、G,连接EC交BD于H.(1)若E为AB的中点,BD=4,求EF的长;
(2)求证:FH=DH+$\frac{1}{2}$BE.
分析 (1)先证明△ABC为等边三角形,得到AB=BD=4,进而求得BE=2,在Rt△EBF中,∠EBF=60°,得到∠BEF=30°,求出BF=$\frac{1}{2}$BE=1.再利用勾股定理即可解答;
(2)取FM=BF,由EF⊥BM,BF=FM,知BE=EM=CD,再证明△EMH≌△CDH,得到DH=HM,从而FH=FM+MH=BF+DH=$\frac{1}{2}$BE+DH.
解答 解:(1)∵∠A=60°,AD=AB,
∴△ABC为等边三角形,
∴AB=BD=4,
∵E为AB的中点,
∴BE=2,
在Rt△EBF中,∠EBF=60°,
∴∠BEF=30°
∴BF=$\frac{1}{2}$BE=1.
∴EF=$\sqrt{B{E}^{2}-B{F}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
(2)如图,取FM=BF,由EF⊥BM,BF=FM,知BE=EM=CD,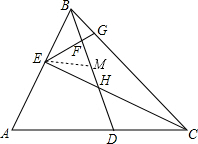
又∵∠BEF=∠FEM=30°,
∴∠BEM=∠A=60°,
∴EM∥AC,
∴∠MEH=∠HCD,∠EHM=∠CHD,
在△EMH和△CDH中,
$\left\{\begin{array}{l}{∠MEH=∠HCD}\\{EM=CD}\\{∠EHM=∠CHD}\end{array}\right.$
∴△EMH≌△CDH,
∴DH=HM,
∴FH=FM+MH=BF+DH=$\frac{1}{2}$BE+DH.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是作出辅助线,构建全等三角形.

练习册系列答案
相关题目
20.某地区连续5天的最高气温(单位:℃)分别是30,33,24,29,24.这组数据的中位数是( )
| A. | 24 | B. | 27 | C. | 29 | D. | 30 |
1.丽威办公用品工厂要生产280个书桌,计划用14天完成任务,当生产任务完成到一半时,发现以后只有每天比原来多生产21个书桌,才能恰好用14天完成任务.设原来平均每天生产x个书桌,下面所列方程正确的是( )
| A. | $\frac{140}{x}$+$\frac{140}{x-21}$=14 | B. | $\frac{140}{x}$+$\frac{140}{x+21}$=14 | C. | $\frac{280}{x}$+$\frac{280}{x+21}$=14 | D. | $\frac{280}{x}$+$\frac{280}{x-21}$=14 |
10.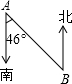 石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
 石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )| A. | 北偏西46° | B. | 北偏西44° | C. | 南偏东46° | D. | 南偏西44° |
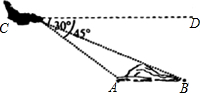 钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73)
钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73) 在正方形ABCD中,点F是对角线AC上任意一点,EF⊥BF交边AD于点E,联结BE.求∠EBF.
在正方形ABCD中,点F是对角线AC上任意一点,EF⊥BF交边AD于点E,联结BE.求∠EBF.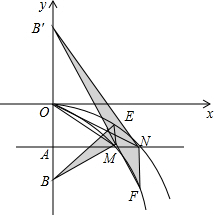 如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.
如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.