题目内容
6．先化简，再求代数式$\frac{a-b}{a}$÷（a-$\frac{2ab-{b}^{2}}{a}$）的值，其中a=-2cos30°，b=2-tan60°．分析 先根据分式混合运算的法则把原式进行化简，再求出a、b的值代入进行计算即可．
解答 解：原式=$\frac{a-b}{a}$÷$\frac{（a-b）^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{（a-b）^{2}}$
=$\frac{1}{a-b}$，
当a=-2cos30°=-2×$\frac{\sqrt{3}}{2}$=-$\sqrt{3}$，b=2-tan60°=2-$\sqrt{3}$时，
原式=$\frac{1}{-\sqrt{3}-（2-\sqrt{3}）}$=-$\frac{1}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
16．某校九（1）班进行了一次体育测试，期中第一小组的成绩分别是（单位：分）30，25，29，28，28，30，29，28，20，28，27，30．这组数据的众数和中位数分别是（ ）
| A． | 28分，28分 | B． | 30分，28分 | C． | 28分，27.5分 | D． | 30分，27.5分 |
17．
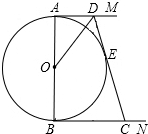如图，AB是⊙O的直径，AM和BN是它的两条切线，DC切⊙O于E，交AM于D，交BN于C．若AD•BC=9，则直径AB的长为（ ）
如图，AB是⊙O的直径，AM和BN是它的两条切线，DC切⊙O于E，交AM于D，交BN于C．若AD•BC=9，则直径AB的长为（ ）| A． | 3$\sqrt{2}$ | B． | 6 | C． | 9 | D． | $\sqrt{13}$ |
14．某水果店计划购进苹果和丑桔共140千克，这两种水果的进价、售价如表所示：
（1）若该水果店购进这两种水果的进货款为1000元，求水果店购进这两种水果各多少千克．
（2）若该水果店决定丑桔的进货量不超过苹果进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？
| 进价（元/千克） | 售价（元/千克） | |
| 苹果 | 5 | 8 |
| 丑桔 | 9 | 13 |
（2）若该水果店决定丑桔的进货量不超过苹果进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？
1．丽威办公用品工厂要生产280个书桌，计划用14天完成任务，当生产任务完成到一半时，发现以后只有每天比原来多生产21个书桌，才能恰好用14天完成任务．设原来平均每天生产x个书桌，下面所列方程正确的是（ ）
| A． | $\frac{140}{x}$+$\frac{140}{x-21}$=14 | B． | $\frac{140}{x}$+$\frac{140}{x+21}$=14 | C． | $\frac{280}{x}$+$\frac{280}{x+21}$=14 | D． | $\frac{280}{x}$+$\frac{280}{x-21}$=14 |
11．
下图中的几何体的左视图是（ ）
下图中的几何体的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
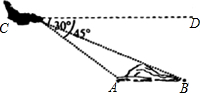钓鱼岛及周边岛屿自古以来就是中国的领土．如图，我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°（己知A、B、C三点在同一平面上），求钓鱼岛南北两端A、B的距离．（参考数据：$\sqrt{3}$=1.73）
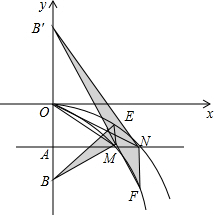如图，在平面直角坐标系中，点A（0，-a2）（a＞0）在y轴的负半轴上，过点A作x轴的平行线，分别交抛物线C1：y=-$\frac{1}{2}$x2（x＞0）于点M，交抛物线C2：y=-$\frac{1}{4}{x}^{2}$（x＞0）于点N，连接OM，ON．