题目内容
9. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )| A. | 5 | B. | 6 | C. | 3 | D. | 4 |
分析 过点P作PE⊥OB于E,根据角平分线上的点到角的两边距离相等可得PE=PD,再根据点到线段的距离的定义解答.
解答  解:如图,过点P作PE⊥OB于E,
解:如图,过点P作PE⊥OB于E,
∵OC是∠AOB的平分线,PD⊥OA,
∴PE=PD=6,
∴点P到边OB的距离为6.
故选B.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
20.若方程(m-2)x2+$\sqrt{m}$x-1=0是关于x的一元二次方程,则( )
| A. | m≠2 | B. | m≥0 | C. | m≥0且m≠2 | D. | m为任意实数 |
4.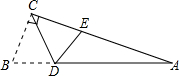 如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的点E处,则∠CED的度数是( )
如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的点E处,则∠CED的度数是( )
 如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的点E处,则∠CED的度数是( )
如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的点E处,则∠CED的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
18.下列三条线段能组成三角形的是( )
| A. | 15,10,8 | B. | 15,23,8 | C. | 10,10,23 | D. | 18,10,8 |
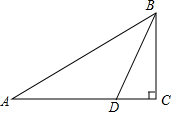 如图,为了测出某塔BC的高度,在塔前的平地上选择一点A,用测角仪测得塔顶B的仰角为30°,在A、C之间选择一点D(A、D、C三点在同一直线上),用测角仪测得塔顶B的仰角为75°,且A、D间的距离为36m.求塔高BC(结果用根号表示).
如图,为了测出某塔BC的高度,在塔前的平地上选择一点A,用测角仪测得塔顶B的仰角为30°,在A、C之间选择一点D(A、D、C三点在同一直线上),用测角仪测得塔顶B的仰角为75°,且A、D间的距离为36m.求塔高BC(结果用根号表示). (1)如图,点B,D都在线段AC上,点D是线段AB的中点,BD=4,BC=2,求线段AC的长度.
(1)如图,点B,D都在线段AC上,点D是线段AB的中点,BD=4,BC=2,求线段AC的长度. 如图所示,已知点A的坐标为(1,0),C,B两点分别在x轴、y轴上移动,且∠1=45°,则点B坐标为(0,-$\sqrt{2}$)时,BC与⊙O相切.
如图所示,已知点A的坐标为(1,0),C,B两点分别在x轴、y轴上移动,且∠1=45°,则点B坐标为(0,-$\sqrt{2}$)时,BC与⊙O相切.