题目内容
19.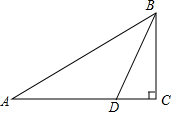 如图,为了测出某塔BC的高度,在塔前的平地上选择一点A,用测角仪测得塔顶B的仰角为30°,在A、C之间选择一点D(A、D、C三点在同一直线上),用测角仪测得塔顶B的仰角为75°,且A、D间的距离为36m.求塔高BC(结果用根号表示).
如图,为了测出某塔BC的高度,在塔前的平地上选择一点A,用测角仪测得塔顶B的仰角为30°,在A、C之间选择一点D(A、D、C三点在同一直线上),用测角仪测得塔顶B的仰角为75°,且A、D间的距离为36m.求塔高BC(结果用根号表示).
分析 先构造出特殊的直角三角形,先求出AE,DE,进而求出BE,即可求出AB,最后即可得出BC.
解答 解:如图,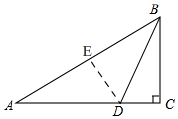 过点D作DE⊥AB,
过点D作DE⊥AB,
∵∠BDC=∠ABD+∠A=75°,∠A=30°,
∴∠ABD=45°,
在Rt△ADE中,∠A=30°,AD=36,
∴DE=$\frac{1}{2}$AD=18,
∴AE=$\sqrt{3}$DE=18$\sqrt{3}$,
在Rt△BDE中,∠ABD=45°,DE=18,
∴BE=DE=18,
∴AB=AE+BE=18$\sqrt{3}$+18,
在Rt△ABC中,∠A=30°,AB=18$\sqrt{3}$+18,
∴BC=$\frac{1}{2}$AB=(9$\sqrt{3}$+9)米.
即:塔高BC为(9$\sqrt{3}$+9)米.
点评 此题是解直角三角形的应用--仰角俯角问题,主要考查的仰角,俯角的定义,解直角三角形,解本题的关键是构造出两个特殊的直角三角形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
7.下列语句正确的是( )
| A. | $\sqrt{64}$的立方根是±2 | B. | $±\frac{8}{7}$是$\frac{64}{49}$的平方根 | ||
| C. | -3是27的负立方根 | D. | (-2 )2的平方根是-2 |
14.已知点A(-3,y1),B(-1,y2),C(2,y3)在函数y=-x2-2x+b的图象上,则y1、y2、y3的大小关系为( )
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
4.△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,且c2-4ac+4a2=0,则sinA+cosA的值为( )
| A. | $\frac{1+\sqrt{3}}{2}$ | B. | $\frac{1+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
8.下列多项式能分解因式的是( )
| A. | x2+y2 | B. | -x2-y2 | C. | x2+4xy+4y2 | D. | x2+xy+y2 |
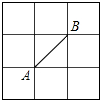 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为轴对称图形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为轴对称图形,则点C的个数是( )
 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )