题目内容
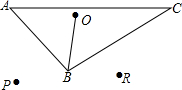 如图,O为△ABC内部一点,OB=3
如图,O为△ABC内部一点,OB=3| 1 |
| 2 |
(1)请指出当∠ABC在什么角度时,会有PR的长度等于7?
(2)承(1)题,请判断当∠ABC不是你指出的角度时,PR的长度是小于7还是大于7?并说明理由.
考点:轴对称的性质,三角形三边关系
专题:
分析:(1)先确定出∠ABC=90°,连接PB、RB,再根据轴对称的性质可得PB=OB,RB=OB,然后求出∠ABP+∠CBR=∠ABC,从而确定出点P、B、R三点共线,即可得解;
(2)根据三角形的任意两边之和大于第三边解答.
(2)根据三角形的任意两边之和大于第三边解答.
解答:解:(1)∠ABC=90°时,PR=7.
理由如下:连接PB、RB,
∵P、R分别为点O关于直线AB、BC对称的点,
∴PB=OB=3
,RB=OB=3
,
∵∠ABC=90°,
∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90°,
∴点P、B、R三点共线,
∴PR=7;
(2)PR的长度小于7.
理由如下:当∠ABC≠90°时,点P、B、R三点不在同一直线上,
所以,PB+BR>PR,
∵PB+BR=2OB=2×3
=7,
所以,PR<7.

理由如下:连接PB、RB,
∵P、R分别为点O关于直线AB、BC对称的点,
∴PB=OB=3
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=90°,
∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90°,
∴点P、B、R三点共线,
∴PR=7;
(2)PR的长度小于7.
理由如下:当∠ABC≠90°时,点P、B、R三点不在同一直线上,
所以,PB+BR>PR,
∵PB+BR=2OB=2×3
| 1 |
| 2 |
所以,PR<7.
点评:本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等;三角形的三边关系.

练习册系列答案
相关题目
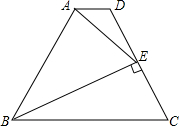 如图,在梯形ABCD中,AD∥BC,BE⊥CD,垂足为点E,连结AE,∠AEB=∠C,且cos∠C=
如图,在梯形ABCD中,AD∥BC,BE⊥CD,垂足为点E,连结AE,∠AEB=∠C,且cos∠C= 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧.