题目内容
 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧.(1)直接写出该圆弧所在圆的圆心D的坐标.
(2)连结AC,求线段AC和弧AC围成的图形的面积(结果保留π).
考点:垂径定理,勾股定理,扇形面积的计算
专题:
分析:(1)利用垂径定理的知识可得:作线段AB与BC的垂直平分线,交点即为点D,继而可求得圆心D的坐标;
(2)利用勾股定理求得⊙D的半径;然后证得△ADF≌△DCG,则可得∠ADC=90°,然后由S=S扇形-S△ADC即可求得答案.
(2)利用勾股定理求得⊙D的半径;然后证得△ADF≌△DCG,则可得∠ADC=90°,然后由S=S扇形-S△ADC即可求得答案.
解答: 解:(1)如图,作线段AB与BC的垂直平分线,交点即为点D,
解:(1)如图,作线段AB与BC的垂直平分线,交点即为点D,
则圆心D的坐标为:(2,0);
(2)连接AD,DC,
则AD=
=
=
;
在△ADE和△DCF中,
,
∴△ADE≌△DCF(SAS),
∴∠ADE=∠DCF,
∵∠DCF+∠CDF=90°,
∴∠ADE+∠CDF=90°,
即∠ADC=90°,
∴S=S扇形-S△ADC=
-
AD•DC=
-
.
 解:(1)如图,作线段AB与BC的垂直平分线,交点即为点D,
解:(1)如图,作线段AB与BC的垂直平分线,交点即为点D,则圆心D的坐标为:(2,0);
(2)连接AD,DC,
则AD=
| AE2+DE2 |
| 22+12 |
| 5 |
在△ADE和△DCF中,
|
∴△ADE≌△DCF(SAS),
∴∠ADE=∠DCF,
∵∠DCF+∠CDF=90°,
∴∠ADE+∠CDF=90°,
即∠ADC=90°,
∴S=S扇形-S△ADC=
| 90πAD2 |
| 360 |
| 1 |
| 2 |
| 5π |
| 4 |
| 5 |
| 2 |
点评:此题考查了垂径定理、勾股定理以及扇形的面积公式.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,半径为6的圆O中,弦AB垂直于半径OC的中点D,则弦AB的长为( )
如图,半径为6的圆O中,弦AB垂直于半径OC的中点D,则弦AB的长为( )| A、4 | ||
| B、5 | ||
C、3
| ||
D、6
|
抛物线y=a(x-3)2+4交y轴于点C,BC∥x轴交抛物线于点B,则线段BC的长为( )
| A、3 | B、6 | C、3a | D、6a |
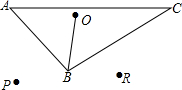 如图,O为△ABC内部一点,OB=3
如图,O为△ABC内部一点,OB=3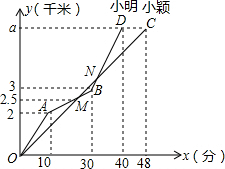 为参加某市冬季越野赛,小明、小强两名同学进行了a千米的越野跑训练,在越野跑训练中的路程y(千米)与时间x(分)函数关系如图所示.
为参加某市冬季越野赛,小明、小强两名同学进行了a千米的越野跑训练,在越野跑训练中的路程y(千米)与时间x(分)函数关系如图所示.