题目内容
诗云：“远望巍巍塔七层，灯光点点倍加增，共灯三百八十一，试问尖头几盏灯？”请回答： ．
考点：一元一次方程的应用
专题：
分析：要求尖头几盏灯，就要先设出求知数，再根据倍加增求出各层的灯数，然后根据共灯三百八十一的等量关系列出方程求解．
解答：解：设顶层有x盏灯．
根据题意得：x+2x+4x+8x+16x+32x+64x=381，
解得：x=3．
因此尖头（最顶层）有3盏灯．
故答案为：3盏灯．
根据题意得：x+2x+4x+8x+16x+32x+64x=381，
解得：x=3．
因此尖头（最顶层）有3盏灯．
故答案为：3盏灯．
点评：本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
| x+1 |
| 2 |
| 2x-1 |
| 3 |
| x+2 |
| 6 |
| A、3x+1-4x-1=1-x+2 |
| B、3（x+1）-2（2x-1）=1-（x+2） |
| C、3（x+1）-2（2x-1）=6-（x+2） |
| D、3（x+1）-4x-1=1-（x+2） |
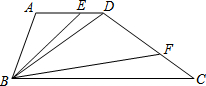如图，在梯形ABCD中，AD∥BC，AD=AB，∠ABC=2∠C，E与F分别为边AD与DC上的两点，且有∠EBF=∠C．
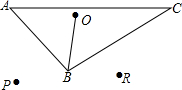如图，O为△ABC内部一点，OB=3
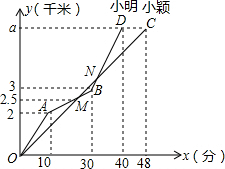为参加某市冬季越野赛，小明、小强两名同学进行了a千米的越野跑训练，在越野跑训练中的路程y（千米）与时间x（分）函数关系如图所示．