题目内容
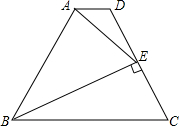 如图,在梯形ABCD中,AD∥BC,BE⊥CD,垂足为点E,连结AE,∠AEB=∠C,且cos∠C=
如图,在梯形ABCD中,AD∥BC,BE⊥CD,垂足为点E,连结AE,∠AEB=∠C,且cos∠C=| 2 |
| 5 |
考点:梯形,相似三角形的判定与性质,解直角三角形
专题:
分析:作AF∥DC,交BE于G,BC于F,作FH∥BE,交DC于H,先求得四边形ABCD是平行四边形,四边形EGFH是矩形,从而求得FC=AD=1,GE=FH,由cos∠C=
求得CH,然后根据勾股定理求得FH,最后根据cos∠AEB=
即可求得AE的长.
| 2 |
| 5 |
| 2 |
| 5 |
解答: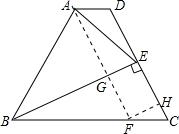 解:作AF∥DC,交BE于G,BC于F,作FH∥BE,交DC于H,
解:作AF∥DC,交BE于G,BC于F,作FH∥BE,交DC于H,
∵AD∥BC,BE⊥CD,
∴四边形ABCD是平行四边形,FH⊥DC,AF⊥BE,
∴FC=AD=1,∠FHC=90°,∠AG,E=90°,
∵cos∠C=
=
,
∴HC=
,
∴FH=
=
,
∵FH⊥DC,AF⊥BE,BE⊥CD,
∴四边形EGFH是矩形,
∴GE=FH=
,
∴cos∠AEB=
,
∵∠AEB=∠C,且cos∠C=
,
∴cos∠AEB=
=
,
∴AE=
=
=
.
故答案为
.
 解:作AF∥DC,交BE于G,BC于F,作FH∥BE,交DC于H,
解:作AF∥DC,交BE于G,BC于F,作FH∥BE,交DC于H,∵AD∥BC,BE⊥CD,
∴四边形ABCD是平行四边形,FH⊥DC,AF⊥BE,
∴FC=AD=1,∠FHC=90°,∠AG,E=90°,
∵cos∠C=
| HC |
| FC |
| 2 |
| 5 |
∴HC=
| 2 |
| 5 |
∴FH=
| FC2-HC2 |
| ||
| 5 |
∵FH⊥DC,AF⊥BE,BE⊥CD,
∴四边形EGFH是矩形,
∴GE=FH=
| ||
| 5 |
∴cos∠AEB=
| GE |
| AE |
∵∠AEB=∠C,且cos∠C=
| 2 |
| 5 |
∴cos∠AEB=
| GE |
| AE |
| 2 |
| 5 |
∴AE=
| 5GE |
| 2 |
5×
| ||||
| 2 |
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了梯形的性质,平行四边形的判定和性质,矩形的判定和性质,勾股定理的应用,解直角三角形等,作出辅助线关键直角三角形、平行四边形、矩形是本题的关键.

练习册系列答案
相关题目
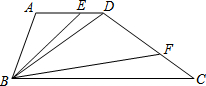 如图,在梯形ABCD中,AD∥BC,AD=AB,∠ABC=2∠C,E与F分别为边AD与DC上的两点,且有∠EBF=∠C.
如图,在梯形ABCD中,AD∥BC,AD=AB,∠ABC=2∠C,E与F分别为边AD与DC上的两点,且有∠EBF=∠C.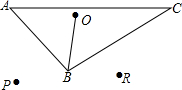 如图,O为△ABC内部一点,OB=3
如图,O为△ABC内部一点,OB=3