题目内容
（1）化简：（a+b）2+（a-b）（a+b）-2ab；
（2）已知（x+y）2=25，（x-y）2=9，求xy与x2+y2的值．
（2）已知（x+y）2=25，（x-y）2=9，求xy与x2+y2的值．
考点：整式的混合运算,完全平方公式
专题：计算题
分析：（1）原式利用完全平方公式及平方差公式化简，去括号合并即可得到结果；
（2）已知等式利用完全平方公式展开，相加相减即可求出所求式子的值．
（2）已知等式利用完全平方公式展开，相加相减即可求出所求式子的值．
解答：解：（1）原式=a2+2ab+b2+a2-b2-2ab=2a2；
（2）∵（x+y）2=x2+y2+2xy=25①，（x-y）2=x2+y2-2xy=9②，
∴①-②得：4xy=16，即xy=4；
①+②得：2（x2+y2）=34，即x2+y2=17．
（2）∵（x+y）2=x2+y2+2xy=25①，（x-y）2=x2+y2-2xy=9②，
∴①-②得：4xy=16，即xy=4；
①+②得：2（x2+y2）=34，即x2+y2=17．
点评：此题考查了整式的混合运算，以及完全平方公式，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
| x+1 |
| 2 |
| 2x-1 |
| 3 |
| x+2 |
| 6 |
| A、3x+1-4x-1=1-x+2 |
| B、3（x+1）-2（2x-1）=1-（x+2） |
| C、3（x+1）-2（2x-1）=6-（x+2） |
| D、3（x+1）-4x-1=1-（x+2） |
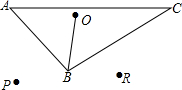如图，O为△ABC内部一点，OB=3