题目内容
2. 已知△ABC为等边三角形,点D、E分别在线段BC、CA上,且CE=BD.直线AD与BE相交于点M.求证:
已知△ABC为等边三角形,点D、E分别在线段BC、CA上,且CE=BD.直线AD与BE相交于点M.求证:①△ABD≌△BCE;②∠AME=60°.
分析 ①根据等边三角形性质得出AB=BC,∠ABD=∠C=60°,再根据SAS可得△ABD≌△BCE;
②根据全等三角形的性质推出∠BAD=∠CBE,再通过三角形外角性质即可求出∠AME的度数.
解答 证明:①∵△ABC为等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴AD=BE.
②∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠AME=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
点评 本题主要考查了等边三角形的性质以及全等三角形的判定及性质问题,能求出△ABD≌△BCE是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.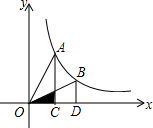 如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
 如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
 如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D. 如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且CD=$\frac{1}{2}$AB,DE⊥CF于E.求证:CE=EF.
如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且CD=$\frac{1}{2}$AB,DE⊥CF于E.求证:CE=EF. 如图,在△ABC中,∠1=∠2,BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.求证:∠B=∠C.
如图,在△ABC中,∠1=∠2,BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.求证:∠B=∠C.