题目内容
16.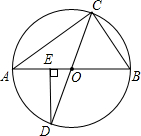 如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB,垂足为E,BC=1,AC=$\sqrt{3}$,求∠D的度数.
如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB,垂足为E,BC=1,AC=$\sqrt{3}$,求∠D的度数.
分析 由AB是直径,推出∠ACB=90°,由BC=1,AC=$\sqrt{3}$,推出tan∠B=$\frac{AC}{BC}$=$\sqrt{3}$,推出∠B=60°,由OB=OC,推出△OBC是等边三角形,由此即可解决问题.
解答 解: ∵AB是直径,
∵AB是直径,
∴∠ACB=90°,
∵BC=1,AC=$\sqrt{3}$,
∴tan∠B=$\frac{AC}{BC}$=$\sqrt{3}$,
∴∠B=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠DOE=∠BOC=60°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠D=90°-∠DOE=30°.
点评 本题考查三角形的外接圆与外心、等边三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识,学会寻找特殊三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | $\root{3}{-8}$=-2 |
5.如果点(a,b)在直线y=-x+1上,二次函数y=ax2+bx的图象必经过( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
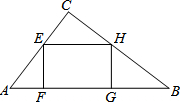 如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.
如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x. 将5个大小相同的圆板如图放置,要求一刀切下,将5个圆切成面积相等两部分,应如何切?
将5个大小相同的圆板如图放置,要求一刀切下,将5个圆切成面积相等两部分,应如何切?