��Ŀ����
6����֪����ͼ1���ڡ�AOB�У�OA=AB=$\sqrt{5}$��BO=2����B��x���ϣ�ֱ��l1��y=kx+3��kΪ��������k��0������A������x�ᡢy��ֱ��ڵ�D��C��ֱ��l2��y=ax��aΪ��������a��0����ֱ��l1���ڵ�P���ҡ�DOP�����Ϊ$\frac{15}{2}$����1����ֱ��l1��l2�Ľ���ʽ��
��2����ͼ2��ֱ��l3��y�ᣬ��ֱ��l1��x��ֱ��ڵ�M��Q����ֱ��l3���߶�OA���߶�OP���ڵ�N������Q�ĺ�����Ϊm��-1��m��2�������APN�����S����m�ĺ�����ϵʽ��

���� ��1�����������A�����꣬����ֱ��l1�Ľ���ʽ���k�������������ε������ʽ�����P�������꣬�ɵõ�P���꣬���ô���ϵ�������ɽ�����⣮
��2����ͼ����PN�����������ٵ�-1��m��0ʱ���ڵ�0��m��2ʱ���ֱ���⼴�ɣ�
��� �⣺��1����ͼ1�У���AM��OB��M��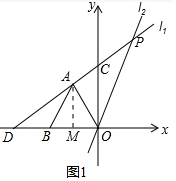
��AB=AO=$\sqrt{5}$��OB=2��AM��OB��
��BM=OM=1��
��Rt��AOM��AM=$\sqrt{O{A}^{2}-O{M}^{2}}$=2��
��A��-1��2������A��-1��2������y=kx+3�õ���2=-k+3�����k=1��
��ֱ��l1�Ľ���ʽΪy=x+3��
��D��-3��0�������P��������m��n����
������$\frac{1}{2}$��3��n=$\frac{15}{2}$��
���n=5��
��m+3=5��
���m=2��
��P��2��5������P��2��5������y=ax���õ�5=2a�����a=$\frac{5}{2}$��
��ֱ��l2�Ľ���ʽΪy=$\frac{5}{2}$x��
��2����ͼ����PN��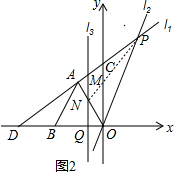
�ٵ�-1��m��0ʱ��M��m��m+3����
��ֱ��OA�Ľ���ʽΪy=-2x��
��N��m��-2m����
��S=$\frac{1}{2}$•MN•��Px-Ax��=$\frac{1}{2}$•��m+3+2m��•3=$\frac{9}{2}$m+$\frac{9}{2}$��
�ڵ�0��m��2ʱ��N��m��$\frac{5}{2}$m����M��m��m+3����
��S=$\frac{1}{2}$•MN•��Px-Ax��=$\frac{1}{2}$•��m+3-$\frac{5}{2}$m��•3=-$\frac{9}{2}$m+$\frac{9}{2}$��
����������S=$\left\{\begin{array}{l}{\frac{9}{2}m+\frac{9}{2}}&{��-1��m��0��}\\{-\frac{9}{2}m+\frac{9}{2}}&{��0��m��2��}\end{array}\right.$��
���� ���⿼��һ�κ����ۺ��⡢����ϵ�����������ε������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ò�����ʾ�й��߶Σ����Ӧ�������ε������ʽ�������п�ѹ���⣮

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�| A�� | 7��8��15 | B�� | 20��15��8 | C�� | 5��15��8 | D�� | 5��7��13 |
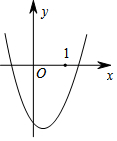 һ�����ߵ�ͼ����ͼ��ʾ�������н����У���ȷ���ǣ�������
һ�����ߵ�ͼ����ͼ��ʾ�������н����У���ȷ���ǣ�������| A�� | a��0 | B�� | ab��0 | C�� | ac��0 | D�� | 2a+b��0 |
| A�� | ��0��3�� | B�� | ��1��1�� | C�� | ��2��1�� | D�� | ��-1��5�� |
| A�� | $\frac{3}{2}$��k��3 | B�� | 2��k��3 | C�� | 2��k��3 | D�� | $\frac{3}{2}$��k��2 |
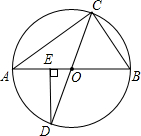 ��ͼ����ABC�ڽ��ڡ�O��AB��CDΪ��O��ֱ����DE��AB������ΪE��BC=1��AC=$\sqrt{3}$�����D�Ķ�����
��ͼ����ABC�ڽ��ڡ�O��AB��CDΪ��O��ֱ����DE��AB������ΪE��BC=1��AC=$\sqrt{3}$�����D�Ķ�����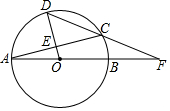 ��ͼ��AB�ǡ�O��ֱ����D��$\widehat{AC}$��һ�㣬��OD����AC���е�E������DC���ӳ���AB���ӳ����ڵ�F��
��ͼ��AB�ǡ�O��ֱ����D��$\widehat{AC}$��һ�㣬��OD����AC���е�E������DC���ӳ���AB���ӳ����ڵ�F��