题目内容
8.若四边形ABCD的对角线BD=AC,且AC与BD互相平分于点O,则四边形ABCD是矩形,若∠AOB=60°,则AB:AC=1:2.分析 首先证明四边形ABCD是平行四边形,由BD=AC,得出四边形ABCD是矩形;得出∠ABC=90°,OA=OB=OC=OD,证明△AOB是等边三角形,得出∠BAC=60°,∠ACB=30°,由直角三角形的性质得出AC=2AB,即可得出结果.
解答 解:如图所示: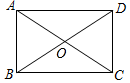
∵四边形ABCD的对角线AC与BD互相平分,
∴四边形ABCD是平行四边形,
又∵BD=AC,
∴四边形ABCD是矩形;
∴∠ABC=90°,OA=OB=OC=OD,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴∠BAC=60°,
∴∠ACB=30°,
∴AC=2AB,
∴AB:AC=1:2;
故答案为:矩,1:2.
点评 本题考查了平行四边形的判定、矩形的判定与性质、等边三角形的判定与性质、直角三角形的性质;熟练掌握矩形的判定与性质是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列语句正确的个数是( )
①两条直线相交有两个角是直角,那么这两条直线垂直;
②若两条直线互相垂直,则相交所成的四个角都是直角;
③互相垂直的两条直线的交点叫做垂直;
④平面内,两条互相垂直的线段不一定相交,但它们所在的直线一定相交.
①两条直线相交有两个角是直角,那么这两条直线垂直;
②若两条直线互相垂直,则相交所成的四个角都是直角;
③互相垂直的两条直线的交点叫做垂直;
④平面内,两条互相垂直的线段不一定相交,但它们所在的直线一定相交.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )
| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ | D. | 2+$\sqrt{3}$或2-$\sqrt{3}$ |
20.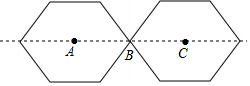 如图是一个中心对称图形,它的对称中心是( )
如图是一个中心对称图形,它的对称中心是( )
 如图是一个中心对称图形,它的对称中心是( )
如图是一个中心对称图形,它的对称中心是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点A或点C |
18.下列各点中,在直线y=2x-3上的是( )
| A. | (0,3) | B. | (1,1) | C. | (2,1) | D. | (-1,5) |
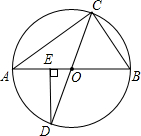 如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB,垂足为E,BC=1,AC=$\sqrt{3}$,求∠D的度数.
如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB,垂足为E,BC=1,AC=$\sqrt{3}$,求∠D的度数. 如图,线段AB=10cm,点C为线段AB上任意一点,点M为AC的中点,点N为BC的中点,则MN=5cm.
如图,线段AB=10cm,点C为线段AB上任意一点,点M为AC的中点,点N为BC的中点,则MN=5cm.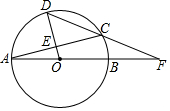 如图,AB是⊙O的直径,D是$\widehat{AC}$上一点,且OD经过AC的中点E,连接DC并延长交AB的延长线于点F.
如图,AB是⊙O的直径,D是$\widehat{AC}$上一点,且OD经过AC的中点E,连接DC并延长交AB的延长线于点F.