题目内容
6.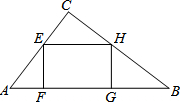 如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.
如图,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,点E在边AC上,过点E作EF⊥AB交AB于点F,EH∥AB交BC于点H,边点H作HG⊥AB于点G,设EF=x.(1)当x为何值时,△AEF与△CEH全等,并说明理由;
(2)点P为EH上一点,且∠FPG=90°,求x的取值范围.
分析 (1)由△AFE∽△ACB,推出$\frac{AE}{AB}$=$\frac{EF}{BC}$=$\frac{AF}{AC}$,推出$\frac{AE}{10}$=$\frac{x}{8}$=$\frac{AF}{6}$,推出AE=$\frac{5}{4}$x,AF=$\frac{3}{4}$x,EC=6-$\frac{5}{4}$x,由△AEF与△CEH全等,∠A=∠CEH,推出EC=AF,可得6-$\frac{5}{4}$x=$\frac{3}{4}$x,解方程即可.
(2)以FG为直径作⊙O,作OM⊥EH于M.当OM≤OF时,EH上存在点P,使得∠FPG=90°,列出不等式即可解决问题.
解答 解:(1)在Rt△ABC中,∵BC=10,sinB=$\frac{3}{5}$,
∴AC=6,BC=8,
∵∠A=∠A.∠AFE=∠C=90°,
∴△AFE∽△ACB,
∴$\frac{AE}{AB}$=$\frac{EF}{BC}$=$\frac{AF}{AC}$,
∴$\frac{AE}{10}$=$\frac{x}{8}$=$\frac{AF}{6}$,
∴AE=$\frac{5}{4}$x,AF=$\frac{3}{4}$x,EC=6-$\frac{5}{4}$x,
∵△AEF与△CEH全等,∠A=∠CEH,
∴EC=AF,
∴6-$\frac{5}{4}$x=$\frac{3}{4}$x,
∴x=3.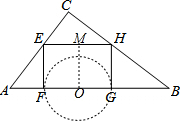
(2)以FG为直径作⊙O,作OM⊥EH于M.
当OM≤OF时,EH上存在点P,使得∠FPG=90°,
∵△CEH∽△CAB,
∴$\frac{CE}{CA}$=$\frac{EH}{AB}$,
∴EH=$\frac{5}{3}$(6-$\frac{5}{4}$x),
∴x≤$\frac{1}{2}$($\frac{5}{3}$(6-$\frac{5}{4}$x),
∴x≤$\frac{120}{49}$,∵x>0,
∴0<x≤$\frac{120}{49}$.
点评 本题考查相似三角形的判定和性质、矩形的性质、解直角三角形、圆的有关知识,解题的关键是学会用方程的思想思考问题,学会利用辅助圆解决直角问题,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 105元 | B. | 108元 | C. | 110元 | D. | 118元 |
①两条直线相交有两个角是直角,那么这两条直线垂直;
②若两条直线互相垂直,则相交所成的四个角都是直角;
③互相垂直的两条直线的交点叫做垂直;
④平面内,两条互相垂直的线段不一定相交,但它们所在的直线一定相交.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\frac{{a}^{2016}}{2015}$ | B. | $\frac{{a}^{2016}}{2016}$ | C. | $\frac{{a}^{4030}}{2015}$ | D. | $\frac{{a}^{4032}}{2016}$ |
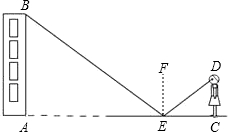 小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)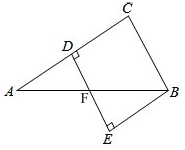 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是18$\sqrt{3}$.
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是18$\sqrt{3}$.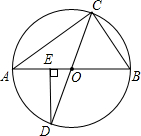 如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB,垂足为E,BC=1,AC=$\sqrt{3}$,求∠D的度数.
如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB,垂足为E,BC=1,AC=$\sqrt{3}$,求∠D的度数.