题目内容
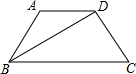 如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为
如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为| 25 |
| 4 |
考点:等腰梯形的性质,算术平均数,众数
专题:
分析:设梯形的四边长为5,5,x,2x,根据平均数求出四边长,求出CN、DN的长,根据勾股定理求出BD即可.
解答:解:∵众数是5,
∴腰长是5,
设梯形的四边长为5,5,x,2x,
则
=
,
解得:x=5,
即等腰梯形的四边长是5,5,5,10,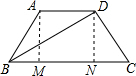
则AB=CD=5,AD=5,BC=10,
过A作AM⊥BC于M,过D作DN⊥BC于N,
则∠DNC=∠DNB=90°,AM∥DN,
∵AD∥BC,
∴四边形AMND是矩形,
∴AD=MN=5,AM=DN,
∵AB=CD,
∴由勾股定理得:BM=CN=
(10-5)=
,
在Rt△DNC中,由勾股定理得:DN=
=
,
在Rt△DNB中,由勾股定理得:BD=
=
=
.
故答案为:
.
∴腰长是5,
设梯形的四边长为5,5,x,2x,
则
| 5+5+x+2x |
| 4 |
| 25 |
| 4 |
解得:x=5,
即等腰梯形的四边长是5,5,5,10,

则AB=CD=5,AD=5,BC=10,
过A作AM⊥BC于M,过D作DN⊥BC于N,
则∠DNC=∠DNB=90°,AM∥DN,
∵AD∥BC,
∴四边形AMND是矩形,
∴AD=MN=5,AM=DN,
∵AB=CD,
∴由勾股定理得:BM=CN=
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△DNC中,由勾股定理得:DN=
52-(
|
| 5 |
| 2 |
| 3 |
在Rt△DNB中,由勾股定理得:BD=
| BN2+DN2 |
(10-
|
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:本题考查了等腰梯形的性质,矩形的性质和判定,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,难度适中.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
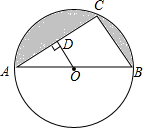 如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.
如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.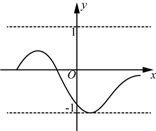 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为 如图,扇形半径OA=10cm,∠AOB=30°,将扇形先绕点B在直线l上向右无滑动翻转,点O第一次再落在l上所经过的路线长是
如图,扇形半径OA=10cm,∠AOB=30°,将扇形先绕点B在直线l上向右无滑动翻转,点O第一次再落在l上所经过的路线长是 如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是
如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是