题目内容
 如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是
如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是考点:圆周角定理,等边三角形的判定与性质
专题:计算题
分析:连结OB、OC,根据圆周角定理得∠BOC=2∠BAC=60°,而OB=OC,于是可判断△OBC为等边三角形,所以OB=BC=1.
解答:解:连结OB、OC,如图,
∵∠BOC=2∠BAC=2×30°=60°,
而OB=OC,
∴△OBC为等边三角形,
∴OB=BC=1,
即⊙O的半径为1.
故答案为1.

∵∠BOC=2∠BAC=2×30°=60°,
而OB=OC,
∴△OBC为等边三角形,
∴OB=BC=1,
即⊙O的半径为1.
故答案为1.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
下列计算正确的是( )
| A、2a+b=2ab |
| B、a3÷a=a2 |
| C、(a-1)2=a2-1 |
| D、(2a)3=6a3 |
若相切两圆⊙O1、⊙O2的圆心距O1O2为13,⊙O1的半径为5,则⊙O2的半径是( )
| A、8 | B、18 |
| C、5或18 | D、8或18 |
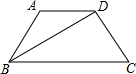 如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为
如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为 如图,已知在矩形ABCD中,AB=2,BC=3,M是边BC的中点,则点D到AM的距离DE等于
如图,已知在矩形ABCD中,AB=2,BC=3,M是边BC的中点,则点D到AM的距离DE等于 如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为
如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为