题目内容
把球放在长方体纸盒内，球的一部分露出盒外，其截面如图，已知EF=CD=80cm，则截面圆的半径为考点：垂径定理的应用,勾股定理
专题：
分析：过点O作OM⊥EF于点M，反向延长OM交BC于点N，连接OF，设OF=r，则OM=80-r，MF=40，然后在Rt△MOF中利用勾股定理求得OF的长即可．
解答：
解：过点O作OM⊥EF于点M，反向延长OM交BC于点N，连接OF，
设OF=x，则OM=80-r，MF=40，
在Rt△OMF中，
∵OM2+MF2=OF2，即（80-r）2+402=r2，解得：r=50cm．
故答案为：50．
解：过点O作OM⊥EF于点M，反向延长OM交BC于点N，连接OF，设OF=x，则OM=80-r，MF=40，
在Rt△OMF中，
∵OM2+MF2=OF2，即（80-r）2+402=r2，解得：r=50cm．
故答案为：50．
点评：本题考查了垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
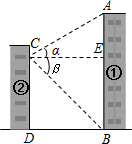某中学九年级学生在学习“直角三角形的边角关系”时，组织开展测量物体高度的实践活动．在活动中，某小组为了测量校园内①号楼AB的高度（如图），站在②号楼的C处，测得①号楼顶部A处的仰角α=30°，底部B处的俯角β=45°，已知两幢楼的水平距离BD为18米，求①号楼AB的高度．（结果保留根号）
如图，点A是⊙O上一点，OA⊥AB，且OA=1，AB=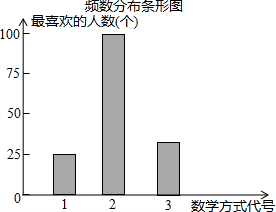
某中学为促进课堂教学，提高教学质量，对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了“频数分布表”和“频数分布条形图”．请你根据图表中提供的信息，解答下列问题．
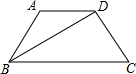如图，四边形ABCD是等腰梯形，若其四边满足长度的众数为5，平均数为
如图，当太阳在A处时，小明测得某树的影长为2米，当太阳在B处时又测得该树的影长为8米．若两次日照的光线互相垂直，则这颗树的高度为