题目内容
如图，已知点B、F、C、E在同一直线上，AB∥DE，AB=DE，BF=EC，请说明△ABC与△DEF全等的理由．考点：全等三角形的判定
专题：
分析：首先根据AB∥DE可得∠B=∠E，然后再根据等式的性质可得BC=EF，进而可利用SAS定理证明△ABC与△DEF全等．
解答：解：因为AB∥DE（已知），
所以∠B=∠E（两直线平行，内错角相等），
因为 BF=EC（已知），
所以BF+FC=EC+CF（等式性质），
即 BC=EF（等量代换），
在△ABC和△DEF中，
，
所以△ABC≌△DEF（SAS）．
所以∠B=∠E（两直线平行，内错角相等），
因为 BF=EC（已知），
所以BF+FC=EC+CF（等式性质），
即 BC=EF（等量代换），
在△ABC和△DEF中，
|
所以△ABC≌△DEF（SAS）．
点评：此题主要考查了全等三角形的判定，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
练习册系列答案
相关题目
如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．
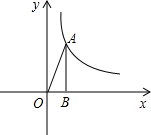如图，点A在双曲线y=