题目内容
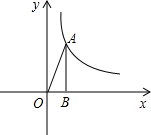 如图,点A在双曲线y=
如图,点A在双曲线y=| k |
| x |
(1)求k的值;
(2)将△AOB绕点O逆时针旋转90°,得到△A′OB′,请在图中画出△A′OB′,并直接写出点A′,B′的坐标;
(3)连接A′B,求直线A′B的表达式.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)根据反比例函数k的几何意义得到S△AOB=
|k|=1,然后去绝对值确定满足条件的k的值;
(2)先利用反比例函数解析式确定A点坐标为(1,2),再根据旋转的定义画出几何图形,然后根据旋转的性质得∠A′B′O=∠ABO=90°,∠B′OB=90°,OB′=OB=1,A′B′=AB=2,再写出点A′,B′的坐标;
(3)利用待定系数法求直线A′B的表达式.
| 1 |
| 2 |
(2)先利用反比例函数解析式确定A点坐标为(1,2),再根据旋转的定义画出几何图形,然后根据旋转的性质得∠A′B′O=∠ABO=90°,∠B′OB=90°,OB′=OB=1,A′B′=AB=2,再写出点A′,B′的坐标;
(3)利用待定系数法求直线A′B的表达式.
解答: 解:(1)根据题意得S△AOB=
解:(1)根据题意得S△AOB=
|k|=1,
∵k>0,
∴k=2;
(2)画图,
反比例函数解析式为y=
,把x=1代入得y=2,则A点坐标为(1,2),
∵△AOB绕点O逆时针旋转90°,得到△A′OB′,
∴∠A′B′O=∠ABO=90°,∠B′OB=90°,OB′=OB=1,A′B′=AB=2,
∴A′点坐标为(-2,1),B′点坐标为(0,1);
(3)设直线A′B的表达式y=kx+b(k≠0),
把A′(-2,1),B (1,0)代入
,解得
,
∴直线A′B的表达式为y=-
x+
.
 解:(1)根据题意得S△AOB=
解:(1)根据题意得S△AOB=| 1 |
| 2 |
∵k>0,
∴k=2;
(2)画图,
反比例函数解析式为y=
| 2 |
| x |
∵△AOB绕点O逆时针旋转90°,得到△A′OB′,
∴∠A′B′O=∠ABO=90°,∠B′OB=90°,OB′=OB=1,A′B′=AB=2,
∴A′点坐标为(-2,1),B′点坐标为(0,1);
(3)设直线A′B的表达式y=kx+b(k≠0),
把A′(-2,1),B (1,0)代入
|
|
∴直线A′B的表达式为y=-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
相关题目
 你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)s(mm2)的反比例函数,其图象如图.
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)s(mm2)的反比例函数,其图象如图. 在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回.甲,乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象如图.当两人的距离不超过3km时,能够用无线对讲机保持联系.甲说:从他们出发
在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回.甲,乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象如图.当两人的距离不超过3km时,能够用无线对讲机保持联系.甲说:从他们出发 △ABC在平面直角坐标系中的位置如图,其中每 个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图,其中每 个小正方形的边长为1个单位长度. 如图,在平面直角坐标系中,抛物线y=
如图,在平面直角坐标系中,抛物线y=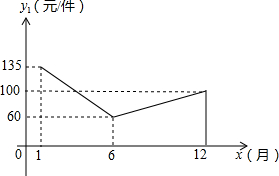
 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,请说明△ABC与△DEF全等的理由.
如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,请说明△ABC与△DEF全等的理由. 如图,在△ABC中,D、E分别是AB、BC的中点.若DE=5,则AC=
如图,在△ABC中,D、E分别是AB、BC的中点.若DE=5,则AC=