题目内容
把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,BC=
+1.斜边AB、DC相交于点O.
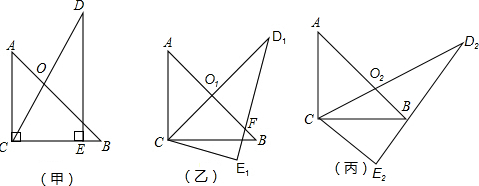
(1)求CO的长;
(2)若把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),这时AB与CD1相交于点O1,此时,
求:CO1的长;
(3)若把三角板D1CE1绕着点C顺时针再旋转15°得△D2CE2(如图丙),这时AB与CD2相交于点O2,此时,求:CO2的长.
| 3 |

(1)求CO的长;
(2)若把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),这时AB与CD1相交于点O1,此时,
求:CO1的长;
(3)若把三角板D1CE1绕着点C顺时针再旋转15°得△D2CE2(如图丙),这时AB与CD2相交于点O2,此时,求:CO2的长.
考点:几何变换综合题
专题:
分析:(1)过点O作OH⊥BC于点H.易知∠HOB=∠B,OH=HB,再求得∠COH=30°,根据直角三角形的性质得OC=2CH,再由三角函数的定义可得HB=OH=
CH.CH+
CH=
+1,求得CH的值,即可得OC;
(2)由题意知∠BCE1=15°,可求得∠O1CB=∠B.由三角形的内角和定理可得∠CO1B=90°,再由三角函数的定义可得CO1=BC•sin∠B;
(3)由于旋转角均为15°,且在乙图中CO1⊥AB,所以CO2与CO在这个旋转过程中关于直线CO1成轴对称.由轴对称的性质得CO2=CO=2.
| 3 |
| 3 |
| 3 |
(2)由题意知∠BCE1=15°,可求得∠O1CB=∠B.由三角形的内角和定理可得∠CO1B=90°,再由三角函数的定义可得CO1=BC•sin∠B;
(3)由于旋转角均为15°,且在乙图中CO1⊥AB,所以CO2与CO在这个旋转过程中关于直线CO1成轴对称.由轴对称的性质得CO2=CO=2.
解答:解:(1)过点O作OH⊥BC于点H.

在Rt△OHB中,∠HOB=90°-∠B=45°=∠B
∴OH=HB.
∵在Rt△DCE中,∠DCE=90°-∠D=60°
∴在Rt△OHC中,∠COH=90°-∠OCH
=90°-60°=30°
∴OC=2CH.
又∵OH=CH•tan∠OCH=
CH,
∴HB=OH=
CH.
又∵CH+HB=CB,
∴CH+
CH=
+1.
∴CH=1.
∴CO=2CH=2;
(2)∵∠BCE1=15°
∴∠O1CB=60°-15°=45°=∠B.
∴∠CO1B=180°-(45°+45°)=90°
∴CO1=BC•sin∠B=
(
+1)=
+
;
(3)从甲图到丙图的过程中,由于旋转角均为15°,且在乙图中CO1⊥AB,所以CO2与CO在这个旋转过程中关于直线CO1成轴对称.
所以CO2=CO=2.

在Rt△OHB中,∠HOB=90°-∠B=45°=∠B
∴OH=HB.
∵在Rt△DCE中,∠DCE=90°-∠D=60°
∴在Rt△OHC中,∠COH=90°-∠OCH
=90°-60°=30°
∴OC=2CH.
又∵OH=CH•tan∠OCH=
| 3 |
∴HB=OH=
| 3 |
又∵CH+HB=CB,
∴CH+
| 3 |
| 3 |
∴CH=1.
∴CO=2CH=2;
(2)∵∠BCE1=15°
∴∠O1CB=60°-15°=45°=∠B.
∴∠CO1B=180°-(45°+45°)=90°
∴CO1=BC•sin∠B=
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
(3)从甲图到丙图的过程中,由于旋转角均为15°,且在乙图中CO1⊥AB,所以CO2与CO在这个旋转过程中关于直线CO1成轴对称.
所以CO2=CO=2.
点评:本题考查了旋转变换的综合题,考查了直角三角形的性质、三角形的内角和定理、三角函数的定义等知识,难度较大.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,D是BC上任意一点(与点B、C不重合),以AD为一边向右侧作等边△ADE,连接CE.求证:
如图,△ABC是等边三角形,D是BC上任意一点(与点B、C不重合),以AD为一边向右侧作等边△ADE,连接CE.求证: 在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回.甲,乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象如图.当两人的距离不超过3km时,能够用无线对讲机保持联系.甲说:从他们出发
在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回.甲,乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象如图.当两人的距离不超过3km时,能够用无线对讲机保持联系.甲说:从他们出发 △ABC在平面直角坐标系中的位置如图,其中每 个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图,其中每 个小正方形的边长为1个单位长度. 如图,在平面直角坐标系中,抛物线y=
如图,在平面直角坐标系中,抛物线y= 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,请说明△ABC与△DEF全等的理由.
如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,请说明△ABC与△DEF全等的理由.