题目内容
为支持抗震救灾,我市A、B两地分别向灾区捐赠物资100吨和180吨.需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨.
(1)求这批赈灾物资运往C、D两县的数量各是多少吨?
(2)设A地运往C县的赈灾物资为x吨(x为整数),若要B地运往C县的赈灾物资数量大于A地运往D县的赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种?
(1)求这批赈灾物资运往C、D两县的数量各是多少吨?
(2)设A地运往C县的赈灾物资为x吨(x为整数),若要B地运往C县的赈灾物资数量大于A地运往D县的赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种?
考点:二元一次方程组的应用,一元一次不等式的应用
专题:
分析:(1)设这批赈灾物资运往C、D两县的数量各是x吨,y吨,根据共有物资280吨,运往C县的数量比运往D县的数量的2倍少80吨,列方程组求解;
(2)根据A地运往C县的赈灾物资数量为x吨,表示出B地运往C县的物资是(160-x)吨,A地运往D县的物资是(100-x)吨,B地运往D县的物资是120-(100-x)=(20+x)吨,然后根据“B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍”列出一个不等式,根据“B地运往D县的赈灾物资数量不超过63吨”列出一个不等式,组成不等式组并求解,再根据x为整数即可得解.
(2)根据A地运往C县的赈灾物资数量为x吨,表示出B地运往C县的物资是(160-x)吨,A地运往D县的物资是(100-x)吨,B地运往D县的物资是120-(100-x)=(20+x)吨,然后根据“B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍”列出一个不等式,根据“B地运往D县的赈灾物资数量不超过63吨”列出一个不等式,组成不等式组并求解,再根据x为整数即可得解.
解答:解:(1)设设这批赈灾物资运往C、D两县的数量各是x吨,y吨,
由题意得,
,
解得:
,
答:运往C,D两县的数量各是160吨,120吨.
(2)设A地运往C县的赈灾物资数量为x吨,则B地运往C县的物资是(160-x)吨,
A地运往D县的物资是(100-x)吨,B地运往D县的物资是120-(100-x)=(20+x)吨,
根据题意得,
,
解不等式①得,x>40,
解不等式②得,x≤43,
所以,不等式组的解集是40<x≤43,
∵x是整数,
∴x取41、42、43,
∴方案共有3种,分别为:
方案一:A地运往C县的赈灾物资数量为41吨,则B地运往C县的物资是119吨,
A地运往D县的物资是59吨,B地运往D县的物资是61吨;
方案二:A地运往C县的赈灾物资数量为42吨,则B地运往C县的物资是118吨,
A地运往D县的物资是58吨,B地运往D县的物资是62吨;
方案三:A地运往C县的赈灾物资数量为43吨,则B地运往C县的物资是117吨,
A地运往D县的物资是57吨,B地运往D县的物资是63吨.
由题意得,
|
解得:
|
答:运往C,D两县的数量各是160吨,120吨.
(2)设A地运往C县的赈灾物资数量为x吨,则B地运往C县的物资是(160-x)吨,
A地运往D县的物资是(100-x)吨,B地运往D县的物资是120-(100-x)=(20+x)吨,
根据题意得,
|
解不等式①得,x>40,
解不等式②得,x≤43,
所以,不等式组的解集是40<x≤43,
∵x是整数,
∴x取41、42、43,
∴方案共有3种,分别为:
方案一:A地运往C县的赈灾物资数量为41吨,则B地运往C县的物资是119吨,
A地运往D县的物资是59吨,B地运往D县的物资是61吨;
方案二:A地运往C县的赈灾物资数量为42吨,则B地运往C县的物资是118吨,
A地运往D县的物资是58吨,B地运往D县的物资是62吨;
方案三:A地运往C县的赈灾物资数量为43吨,则B地运往C县的物资是117吨,
A地运往D县的物资是57吨,B地运往D县的物资是63吨.
点评:本题考查了一元一次不等式组的应用,二元一次方程组的应用,找出题目中的数量关系是解题的关键,(2)难点在于根据A地运往C县的赈灾物资数量为x吨,表示出运往其他县的物资是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回.甲,乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象如图.当两人的距离不超过3km时,能够用无线对讲机保持联系.甲说:从他们出发
在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回.甲,乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象如图.当两人的距离不超过3km时,能够用无线对讲机保持联系.甲说:从他们出发 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,请说明△ABC与△DEF全等的理由.
如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,请说明△ABC与△DEF全等的理由. 如图,O为矩形ABCD对角线的交点,DE∥AC,AE∥BD.
如图,O为矩形ABCD对角线的交点,DE∥AC,AE∥BD.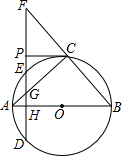 如图,⊙O是△ABC外接圆,AB是⊙O的直径,弦DE⊥AB于点H,DE与AC相交于点G,DE、BC的延长线交于点F,P是GF的中点,连接PC.
如图,⊙O是△ABC外接圆,AB是⊙O的直径,弦DE⊥AB于点H,DE与AC相交于点G,DE、BC的延长线交于点F,P是GF的中点,连接PC.
 如图,在△ABC中,D、E分别是AB、BC的中点.若DE=5,则AC=
如图,在△ABC中,D、E分别是AB、BC的中点.若DE=5,则AC=