题目内容
8.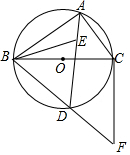 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
分析 (1)欲证明DB=DE,只要证明∠DBE=∠DEB;
(2)欲证明直线CF为⊙O的切线,只要证明BC⊥CF即可;
解答 (1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.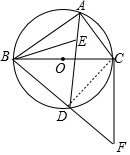
(2)连接CD.
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD,
∵BD=DF,
∴CD=DB=DF,
∴∠BCF=90°,
∴BC⊥CF,
∴CF是⊙O的切线.
点评 本题考查三角形的内切圆与内心、切线的判定、等腰三角形的判定、直角三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
13.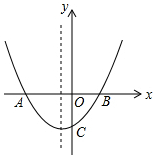 如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b-c=2;②a=$\frac{1}{2}$;③ac=b-1;④$\frac{a+b}{c}$>0
其中正确的个数有( )
 如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:①2b-c=2;②a=$\frac{1}{2}$;③ac=b-1;④$\frac{a+b}{c}$>0
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列实数中,无理数是( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -2 | D. | $\frac{2}{7}$ |
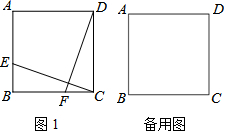

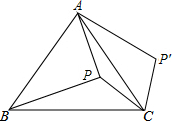 如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为$\frac{3}{5}$.
如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为$\frac{3}{5}$.