题目内容
17.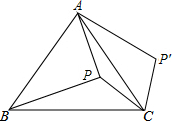 如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为$\frac{3}{5}$.
如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为$\frac{3}{5}$.
分析 连接PP′,如图,先利用旋转的性质得CP=CP′=6,∠PCP′=60°,则可判定△CPP′为等边三角形得到PP′=PC=6,再证明△PCB≌△P′CA得到PB=P′A=10,接着利用勾股定理的逆定理证明△APP′为直角三角形,∠APP′=90°,然后根据正弦的定义求解.
解答 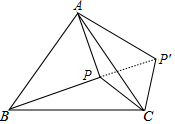 解:连接PP′,如图,
解:连接PP′,如图,
∵线段PC绕点C顺时针旋转60°得到P'C,
∴CP=CP′=6,∠PCP′=60°,
∴△CPP′为等边三角形,
∴PP′=PC=6,
∵△ABC为等边三角形,
∴CB=CA,∠ACB=60°,
∴∠PCB=∠P′CA,
在△PCB和△P′CA中
$\left\{\begin{array}{l}{PC=P′C}\\{∠PCB=∠P′CA}\\{CB=CA}\end{array}\right.$,
∴△PCB≌△P′CA,
∴PB=P′A=10,
∵62+82=102,
∴PP′2+AP2=P′A2,
∴△APP′为直角三角形,∠APP′=90°,
∴sin∠PAP′=$\frac{PP′}{P′A}$=$\frac{6}{10}$=$\frac{3}{5}$.
故答案为$\frac{3}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质和勾股定理的逆定理.

练习册系列答案
相关题目
6.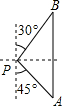 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )| A. | 60$\sqrt{3}$ n mile | B. | 60$\sqrt{2}$ n mile | C. | 30$\sqrt{3}$ n mile | D. | 30$\sqrt{2}$ n mile |
7. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有50人,a+b=28,m=8;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.
 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.调查结果统计表
| 组别 | 分组(单位:元) | 人数 |
| A | 0≤x<30 | 4 |
| B | 30≤x<60 | 16 |
| C | 60≤x<90 | a |
| D | 90≤x<120 | b |
| E | x≥120 | 2 |
(1)填空:这次被调查的同学共有50人,a+b=28,m=8;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.
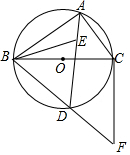 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6<ax+4<kx的解集为1<x<$\frac{5}{2}$.
如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6<ax+4<kx的解集为1<x<$\frac{5}{2}$. 如图,△ABC中,D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于6.
如图,△ABC中,D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于6.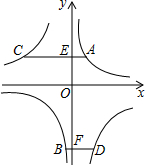 如图,A,B两点在反比例函数y=$\frac{k_1}{x}$的图象上,C,D两点在反比例函数y=$\frac{k_2}{x}$的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是( )
如图,A,B两点在反比例函数y=$\frac{k_1}{x}$的图象上,C,D两点在反比例函数y=$\frac{k_2}{x}$的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是( )