题目内容
16.如图1,在正方形ABCD中,点E,F分别是边AB,BC上的点,且BE=CF.连结CE,DF.将线段FD绕点F逆时针旋转90°,得到线段FG.(1)依题意将图1补全;
(2)连结EG,请判断:EG与CF的数量关系是EG=CF,位置关系是EG∥CF;并证明你的结论;
(3)当FG经过BE中点时,写出求∠CDF度数的思路.
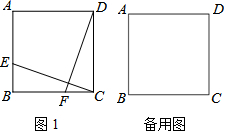
分析 (1)根据要求画出图形即可;
(2)只要证明四边形EGFC是平行四边形即可;
(3)首先证明∠CDF=∠BCE=∠G,求出∠G即可解决问题.
解答 解:(1)如图所示: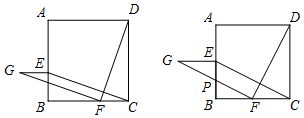 ;
;
(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;
证明:∵正方系ABCD,
∴BC=CD,∠ABC=∠BCD=90°.
∵BE=CF,
∴△BCE≌△CDF
∴DF=CE,∠BEC=∠CFD.
∵∠BCE+∠BEC=90°,
∴∠BCE+∠CFD=90°.
即CE⊥DF,
∵线段FD绕点F逆时针旋转90°,得到线段FG,
∴CE∥FG,DF=FG.
∴CE=FG.
∴四边形GFCE是平行四边形.
∴EG=CF,EG∥CF;
故答案为EG=CF,EG∥CF.
(3)当FG经过BE中点P时,
由△BCE≌△CDF,可得∠CDF=∠BCE.
由□GFCE,可得∠BCE=∠G.
即∠CDF═∠G,
由BE=CF=GE,可得PE=$\frac{1}{2}$GE;
利用锐角三角函数,可求∠G的度数,从而可求∠CDF的度数.
点评 本题考查旋转变换、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质的等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
| x(元) | 200 | 240 | 270 | 300 |
| y(间) | 90 | 70 | 55 | 40 |
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
6.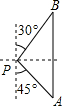 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )| A. | 60$\sqrt{3}$ n mile | B. | 60$\sqrt{2}$ n mile | C. | 30$\sqrt{3}$ n mile | D. | 30$\sqrt{2}$ n mile |
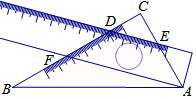 一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为15°.
一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为15°.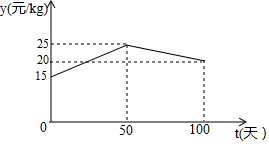 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).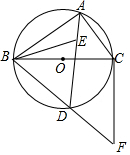 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE. 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6<ax+4<kx的解集为1<x<$\frac{5}{2}$.
如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6<ax+4<kx的解集为1<x<$\frac{5}{2}$.